はじめに

本ブログではこれまでピッチ推定の要素技術について説明してきましたが、一旦それらを組み合わせて、人間の音声データからピッチ推定するツールを作ってみます。自己相関関数で声のピッチを求めるの実践編です。

ピッチ推定ツールの実装

import argparse
import os.path
import numpy
import scipy.io.wavfile
import scipy.fftpack
import scipy.signal

def __lpcms_int16_to_float(lpcms):
    lpcm_array = []
    for index, lpcm in enumerate(lpcms):
        lpcm_array.append(numpy.divide(lpcm.astype(float), 32767.0))
        lpcms = numpy.array(lpcm_array)
    return lpcms

def __read_wave_file_to_float(wave_file_name):
    fs, data = scipy.io.wavfile.read(wave_file_name)
    nch = 1
    if type(data[0]) == numpy.ndarray:
        lpcms = data.transpose()
        nch = len(lpcms)
    else:
        lpcms = numpy.array([data])
    pcm_type_from_file = type(lpcms[0][0])
    if pcm_type_from_file == numpy.int16:
        lpcms = __lpcms_int16_to_float(lpcms)
    return fs, nch, lpcms

def __split_lpcm(lpcm, stride, width):
    n = int(numpy.floor((len(lpcm) - width) / stride))
    extended_length = n * stride + width
    if len(lpcm) < extended_length:
        lpcm = numpy.r_[lpcm, numpy.zeros(extended_length - len(lpcm))]
    splited_lpcms = []
    for index in range(0, n):
        offset = index * stride
        splited_lpcms.append(lpcm[offset:offset + width])
    return numpy.array(splited_lpcms)

def __acf_by_dft(values):
    power_spectrum = numpy.abs(scipy.fftpack.fft(values)) ** 2
    return numpy.real(scipy.fftpack.ifft(power_spectrum))

def __estimate_pitch(fragment, window_function):
    windowed = numpy.multiply(fragment, window_function)
    padded = numpy.r_[windowed, numpy.zeros(len(windowed))]
    acf = __acf_by_dft(padded)[:len(windowed)]
    min_index = numpy.argmin(acf)
    max_index = numpy.argmax(acf[min_index:]) + min_index
    pitch_length = max_index
    pitch_likely = acf[pitch_length] / acf[0]
    return (pitch_length, pitch_likely)

def __freq_to_cent(freq):
    return 1200 * numpy.log2(freq/440) + 6900

def __quantize_cent(cent):
    return ((cent + 50) // 100) * 100

def __output_series_csv_file(output_filepath, series_data, stride):
    csv_rows = [f'{stride * i},{value}' for i, value in enumerate(series_data)]
    with open(output_filepath, "wt") as csv_file:
        csv_file.write("\n".join(csv_rows))
    return None

def __main(input_wave_filepath, window_size, stride):
    fs, nch, lpcms = __read_wave_file_to_float(input_wave_filepath)
    window_half_size = args.window_size // 2
    fragments = __split_lpcm(lpcms[0], stride, window_size)

    pitchs = []
    likelies = []
    window_function = scipy.signal.blackmanharris(window_size)
    for fragment in fragments:
        pitch_length, pitch_likely = __estimate_pitch(fragment, window_function)
        basic_frequency = fs / pitch_length if pitch_length != 0 else 0
        pitchs.append(basic_frequency)
        likelies.append(pitch_likely)

    cents = [__freq_to_cent(pitch) for pitch in pitchs]
    quantaized_cents = [__quantize_cent(cent) for cent in cents]
    basename = os.path.basename(input_wave_filepath)
    __output_series_csv_file(basename + "_pitch.csv", pitchs, stride)
    __output_series_csv_file(basename + "_pitch_r.csv", likelies, stride)
    __output_series_csv_file(basename + "_cent.csv", cents, stride)
    __output_series_csv_file(basename + "_cent_q.csv", quantaized_cents, stride)
    return None

if __name__ == "__main__":
    argment_parser = argparse.ArgumentParser()
    argment_parser.add_argument("-i", "--input_wave_filepath", type=str, required=True)
    argment_parser.add_argument("-w", "--window_size", type=int, default=512)
    argment_parser.add_argument("-s", "--stride", type=int, default=128)
    args = argment_parser.parse_args()

    __main(args.input_wave_filepath, args.window_size, args.stride)

    exit(0)

処理の概要

処理手順は以下の通りです。

WAVEファイルを読み込む
strideサンプルずつずらしながらwindow_sizeサンプル単位で切り出す
切り出した断片毎に窓がけを行う
窓がけの結果が二倍のサンプル数になるように末尾にゼロ値を連結する
ゼロ値連結した結果に対して自己相関関数を求める
自己相関関数から基本周期長を推定する
基本周期長を物理周波数に変換する
断片毎に求めた物理周波数からcent等を算出する
物理周波数やcent等を時系列データとして出力する

コーディングについて

pythonはif文がスコープを作らないので、if __name__ ...のブロックでは引数のパースだけを行い、__main関数を呼び出しています。実際の処理は__main関数から始まります。

実験用ツールなので機能を使い回す事を想定せず、関数は全て非公開関数として__付きで定義しています。

importしているモジュールの使途は以下の通りです。

argparse:コンソール引数のパースとバリデーションに利用しています。
os.path:引数で与えられたファイルパスの加工に利用しています。
numpy:LPCMの切り出しや変換、ベクトル同士のアダマール積等に利用しています。
scipy.io.wavfile:WAVEファイルの読み込みに利用しています。
scipy.fftpack:自己相関関数を求める際のDFTに利用しています。
scipy.signal:窓関数の生成に利用しています。

WAVEファイルを読み込む

def __lpcms_int16_to_float(lpcms):
    lpcm_array = []
    for index, lpcm in enumerate(lpcms):
        lpcm_array.append(numpy.divide(lpcm.astype(float), 32767.0))
        lpcms = numpy.array(lpcm_array)
    return lpcms

def __read_wave_file_to_float(wave_file_name):
    fs, data = scipy.io.wavfile.read(wave_file_name)
    nch = 1
    if type(data[0]) == numpy.ndarray:
        lpcms = data.transpose()
        nch = len(lpcms)
    else:
        lpcms = numpy.array([data])
    pcm_type_from_file = type(lpcms[0][0])
    if pcm_type_from_file == numpy.int16:
        lpcms = __lpcms_int16_to_float(lpcms)
    return fs, nch, lpcms

今回はLPCM値が全てfloat型になっていると都合が良いため、WAVEファイルから読み込んだLPCM配列がfloat型の配列になるように読み込みます。

読み込んだLPCM値の型が符号付き16bit整数だった場合、 $-1.0 \sim 1.0$ の値の範囲になるように__lpcms_int16_to_float関数でスケーリングと型の変換を行います。

符号付き16bit整数の範囲は、2の補数表現の場合だと $-32768 \sim 32767$ ですが、ここでは簡単化のために一律 $32767.0$ で除算してスケーリングしています。これは $-32768$ が入力WAVEファイル内に存在しない事を期待しているためです。逆に $-1.0 \sim 1.0$ の値を符号付き16bit整数に変換する場合を考えると、正負区別なく $32767.0$ をかける事を想定しています。仮に $-1.0 \sim 1.0$ の値を符号付き16bit整数に変換する処理において正値と負値でスケーリング係数を変えてしまうと、波形が歪んでしまいますので、そのような前提には立たないという事です。

LPCMを断片に切り出す

def __split_lpcm(lpcm, stride, width):
    n = int(numpy.floor((len(lpcm) - width) / stride))
    extended_length = n * stride + width
    if len(lpcm) < extended_length:
        lpcm = numpy.r_[lpcm, numpy.zeros(extended_length - len(lpcm))]
    splited_lpcms = []
    for index in range(0, n):
        offset = index * stride
        splited_lpcms.append(lpcm[offset:offset + width])
    return numpy.array(splited_lpcms)

決まった窓幅と歩幅(stride)でLPCMを分割します。分割したLPCMには重複領域が存在する点に注意してください。
今回の処理はピッチの推定であり、切り出した窓単位でピッチ推定行うため、切り出した窓の前後間隔は問題になりません。歩幅は時系列で見た場合にどれだけ密にピッチ推定を行うかを決めるだけのパラメータです。

窓がけ

    window_function = scipy.signal.blackmanharris(window_size)

    windowed = numpy.multiply(fragment, window_function)

窓関数という名の１次元ベクトルを生成し、LPCMの切り出した窓に掛けます。ここでの「窓をかける」は「施す」という意味ではなく「掛け算する(内積ではなくアダマール積)」という意味です。同音異義語なのでややこしいです。

全てのLPCM断片に同じ窓関数を掛けるので、窓関数は一度だけ生成してそれを使いまわしています。
ここで生成した窓関数はブラックマンハリス窓です。バランスが良いので使っていますが、特にこれを使うべきという根拠があって使っているわけではありません。ピッチ推定の場合は分析に都合の良い窓を選べば良いです。

窓関数の周波数特性は畳み込み積分と窓関数で説明しています。

ゼロ値連結と自己相関関数

    padded = numpy.r_[windowed, numpy.zeros(len(windowed))]
    acf = __acf_by_dft(padded)[:len(windowed)]

以前の記事で紹介したゼロ値連結する事で自己相関関数のオーバーラップ部分をなくし、必ずゼロに向かって減衰する自己相関関数を求めるテクニックです。窓長を倍にしている都合で周波数分解能も上がります。自己相関関数の領域で言うと有効な周期長が長くなります。

自己相関関数とDFTの関係は自己相関関数とパワースペクトラムで解説しています。

基本周期長を推定する

    min_index = numpy.argmin(acf)
    max_index = numpy.argmax(acf[min_index:]) + min_index
    pitch_length = max_index
    pitch_likely = acf[pitch_length] / acf[0]
    return (pitch_length, pitch_likely)

自己相関関数の最小値インデックスを求めます。理屈上、この最小値インデックスは基本周期の半周期に相当します。自己相関関数は自信の信号をずらしながら相互相関値を求める事だったので、周期的な信号であれば半周期ずれたところで負の相関が最も強く現れます。

基本周期長は当然ながら基本周期の半周期より長いので（自明すぎて何を言っているのかわからないレベルですが）、半周期である最小値インデックス以降の最大値インデックスが基本周期であると推定できます。

自己相関関数は時間領域の関数であり、インデックスはサンプル数のずれと同じです。つまり、最大値インデックスがそのまま基本周期長のサンプル数です。

また、ここではその時の相関係数acf[pitch_length] / acf[0]も同時に求めてpitch_likelyとしてタプルで値を返しています。相関係数が低い場合、それは期待したピッチではない可能性が高いので、後処理でピッチ誤判定を補正するために使います。

基本周期長から各種の値へ変換する

def __freq_to_cent(freq):
    return 1200 * numpy.log2(freq/440) + 6900

def __quantize_cent(cent):
    return ((cent + 50) // 100) * 100

        basic_frequency = fs / pitch_length if pitch_length != 0 else 0
        pitchs.append(basic_frequency)
        likelies.append(pitch_likely)

    cents = [__freq_to_cent(pitch) for pitch in pitchs]
    quantaized_cents = [__quantize_cent(cent) for cent in cents]

基本周期長をWAVEファイルのサンプリングレートで割れば、一秒に対する周期長、つまり物理的な周波数に変換できます。
あとは音程を把握しやすいように、セントに変換した値、セントをさらに100セント単位で量子化した値を求めておきます。
セントへの変換は周波数をセントへ変換するを参照してください。

時系列出力

    basename = os.path.basename(input_wave_filepath)
    __output_series_csv_file(basename + "_pitch.csv", pitchs, stride)
    __output_series_csv_file(basename + "_pitch_r.csv", likelies, stride)
    __output_series_csv_file(basename + "_cent.csv", cents, stride)
    __output_series_csv_file(basename + "_cent_q.csv", quantaized_cents, stride)

最後に算出した値を時系列データとして出力します。複数の値を出力する場合、出力ファイル名をそれぞれ入力する仕様だと辛いので、入力ファイル名にサフィックスを連結して出力する方法を良く使います。

出力フォーマットは、オフセットサンプル数、その時の値をペアと１行ずつ書き出したCSVファイルです。時系列のCVSデータにする事で、Sonic Visualiserで可視化しやすくなります。

実験

実験データ

ピッチ推定の実験なので、背景音がなるべく少ない独唱音声があると助かります。
今回は以下のWebサイトで配布されているデータを使って実験しました。

JSUT-Song

この配布データに同梱されいているWAVEファイルの内、jsut-song_ver1/child_song/wav/003.wavを対象として実験します。

ツールを実行する

コンソールで以下のようにpythonでスクリプトを実行します。

$ python estimate_pitch.py -i ./jsut-song_ver1/child_song/wav/003.wav

すると、カレントディレクトリに以下のファイルを出力します。

003.wav_cent.csv:時系列セント値
003.wav_cent_q.csv:時系列量子化済セント値
003.wav_pitch.csv:時系列基本周波数
003.wav_pitch_r.csv:時系列ピッチ信頼度

実行結果をグラフで見る

波形ファイルと時系列データの読み込み

003.wavをSonic Visualiserで開きます。そこに追加で003.wav_cent.csvを開きます。
Sonic Visualiserでは、CSVファイルを開く際に１列目をどのように扱うか聞いてきます。本ツールでは時間軸にサンプル数を使っているので、Sonic Visulaiserに読み込ませる際に１列目を「サンプル数」として指定します。そうすると、読み込んだ003.wavの波形データと一致した時間軸でCSVの時系列データをグラフ表示できます。


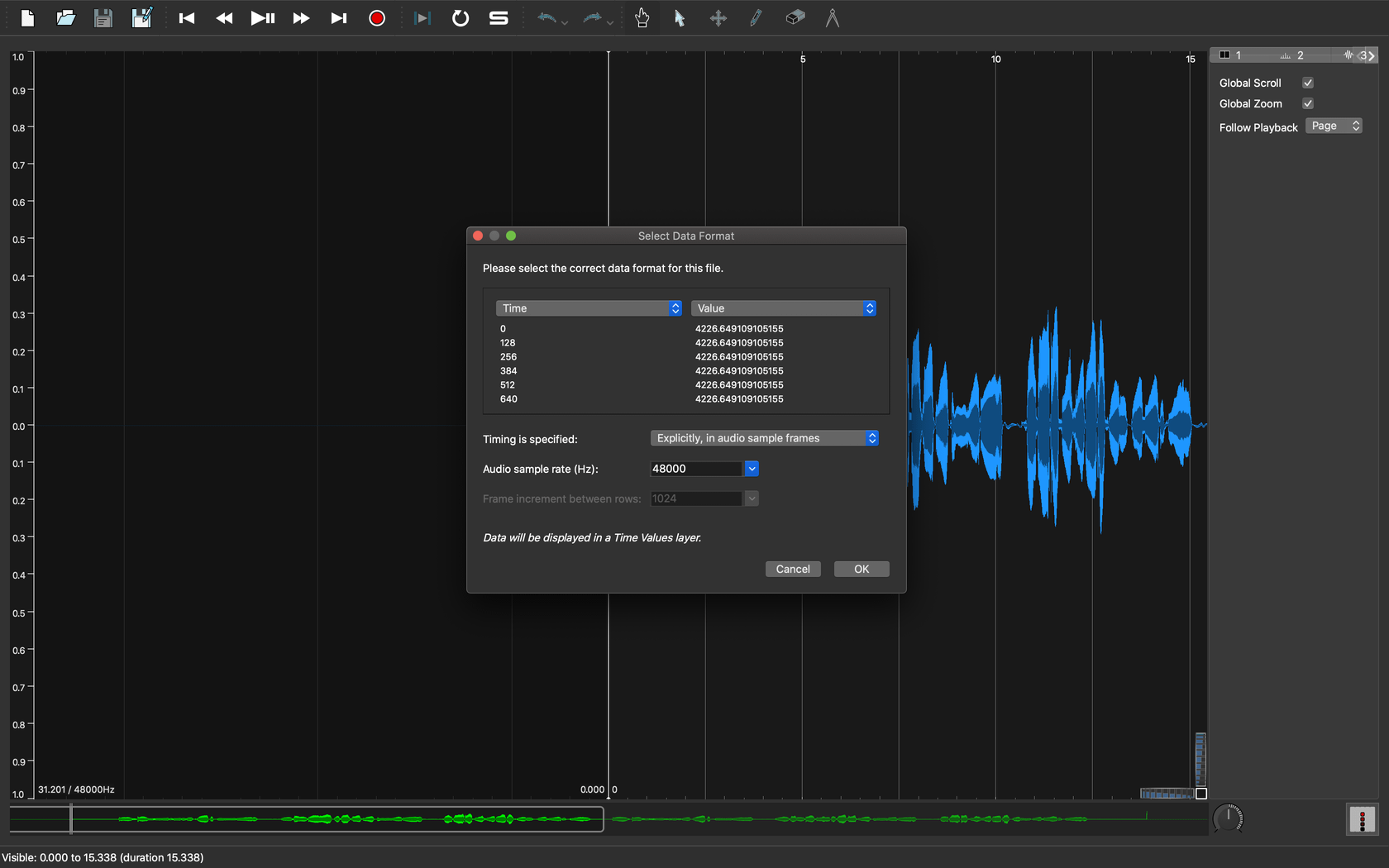図1. サンプル単位の時系列データを読み込む


図2. 003.wav_cent.csvを読み込んだ結果

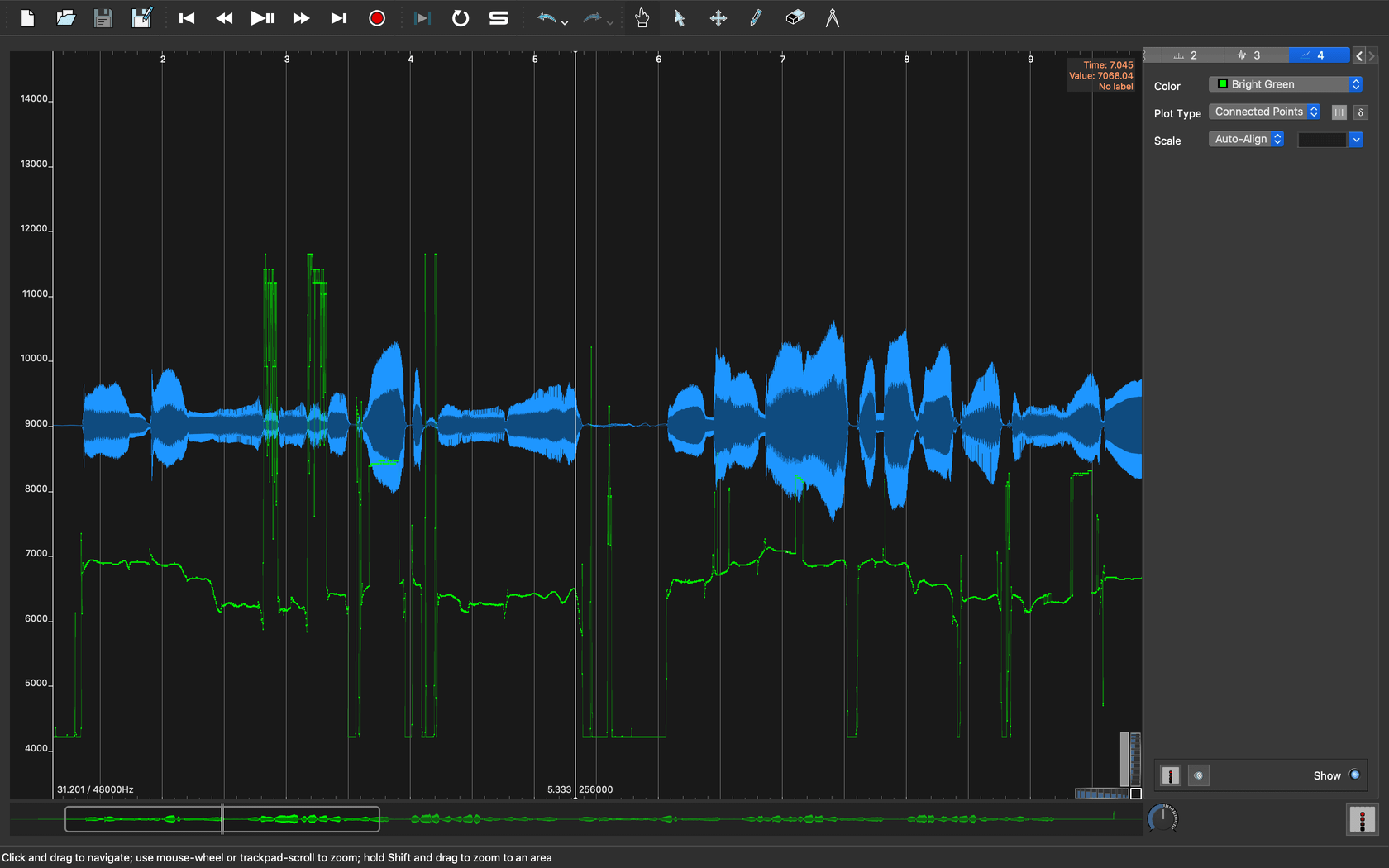
ピッチ信頼度を時系列で記録した003.wav_pitch_r.csvも読み込んでみます。


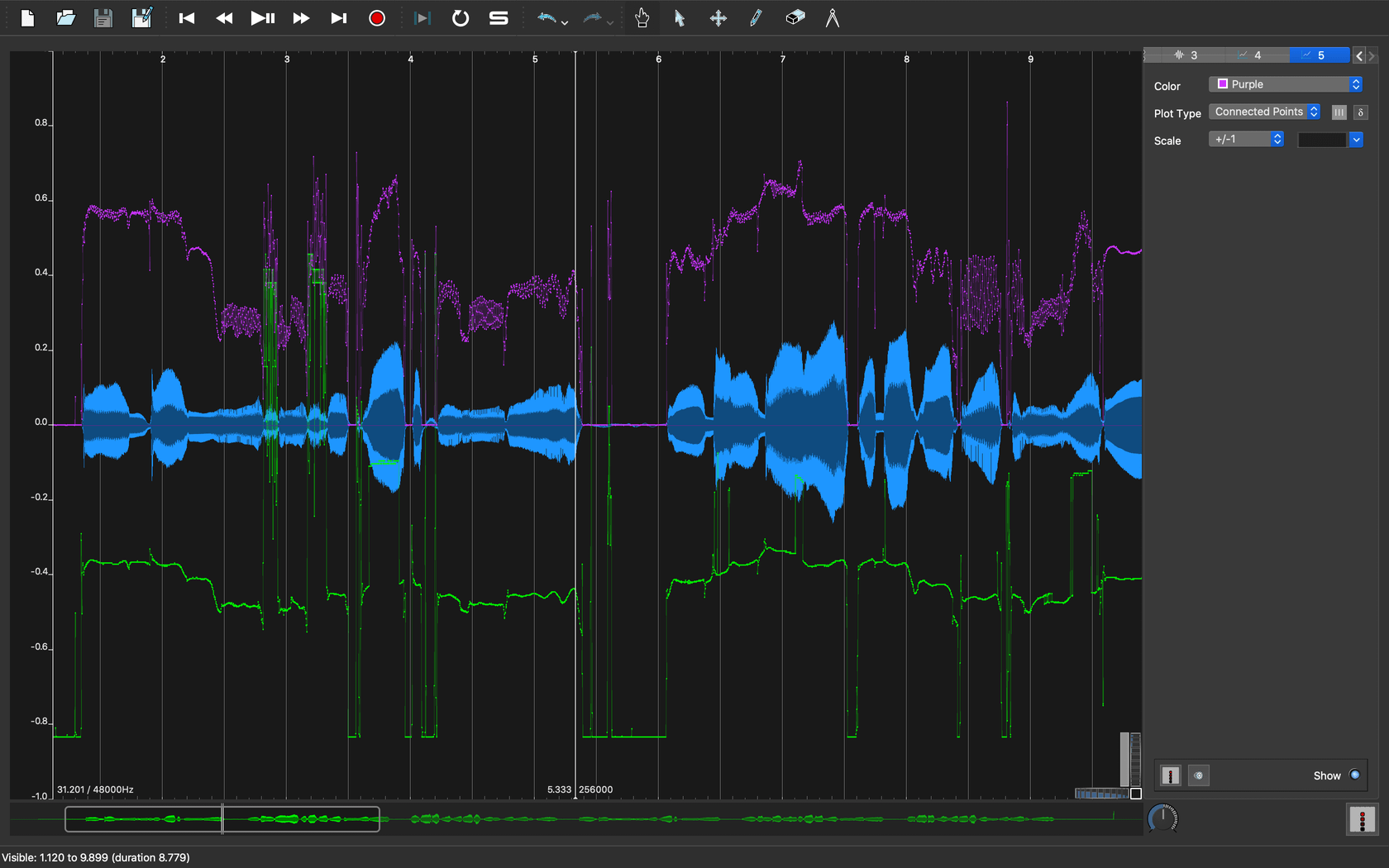図3. ピッチ信頼度を重ねて表示

ピッチ信頼度は相関係数 $-1 \sim 1$ になるようにスケーリングした値なので、表示範囲も $\pm1$ で表示しています。絶対値的な基準は無いですが、 $1$ に近ければピッチとしての信頼度は高いと解釈できます。

グラフを見ると3秒前後でセント値が跳ね上がっているところがあります。波形データを再生して聞いてみると、「でーんでんむーしむし」の「し」の子音部分である事がわかります。日本語の「さしすせそ」の子音は 歯擦音（しさつおん） と言って、閉じた前歯から強く息を吹き出す事で比較的高周波の音になります。この歯擦音の部分でピッチ抽出の結果が暴れてしまっています。音高としてはまず人間の基本周波数的にありえないような高音高ですが、ピッチ信頼度は高めに出てしまっているので弁別は簡単ではなさそうです。

別のケースを見てみます。


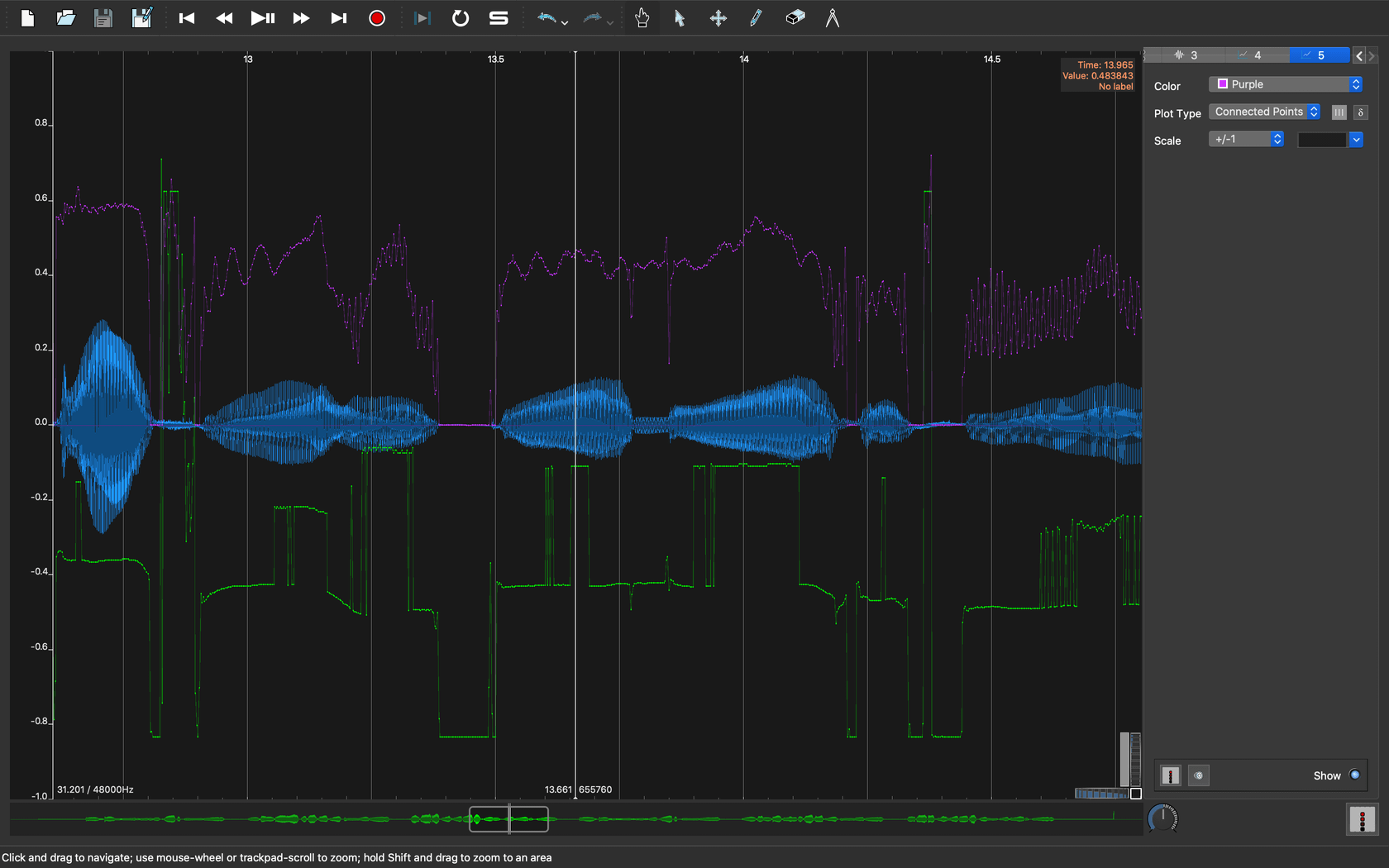図4. ピッチ推定のオクターブミス

約13.5秒付近までスクロールしてグラフを見てみると、比較的ピッチが安定しているはずの母音のロングトーン部分で、ピッチ推定の結果が大きく変動しています。変動の形をみると、これは オクターブミス が生じていると言えそうです。

人間の有声母音は、ノコギリ波のような倍音成分を多量に含む音声を基本波形としているため、エネルギーバランスによっては倍音側を基本周波数と誤推定してしまうことがあります。丁度倍音の位置関係になるので、音階で考えると１オクターブ分のずれになります。このように、本来推定すべきピッチからオクターブ単位でずれてピッチ誤推定することを私は オクターブミス と呼んでいます。

ここまでの実験結果からすると、自己相関関数を用いたピッチ推定法はあまり当てにならないように見えますが、本ツールはまだ変更可能なパラメータがあります。

窓サイズを変える

今度は窓サイズを明示して実行してみましょう。

$ python estimate_pitch.py -i ./jsut-song_ver1/child_song/wav/003.wav -w 2048

結果を先ほどと同じようにSonic Visualiserで読み込み、グラフ表示してみます。
まずは3秒付近の歯擦音がどのように変わったかみてみます。


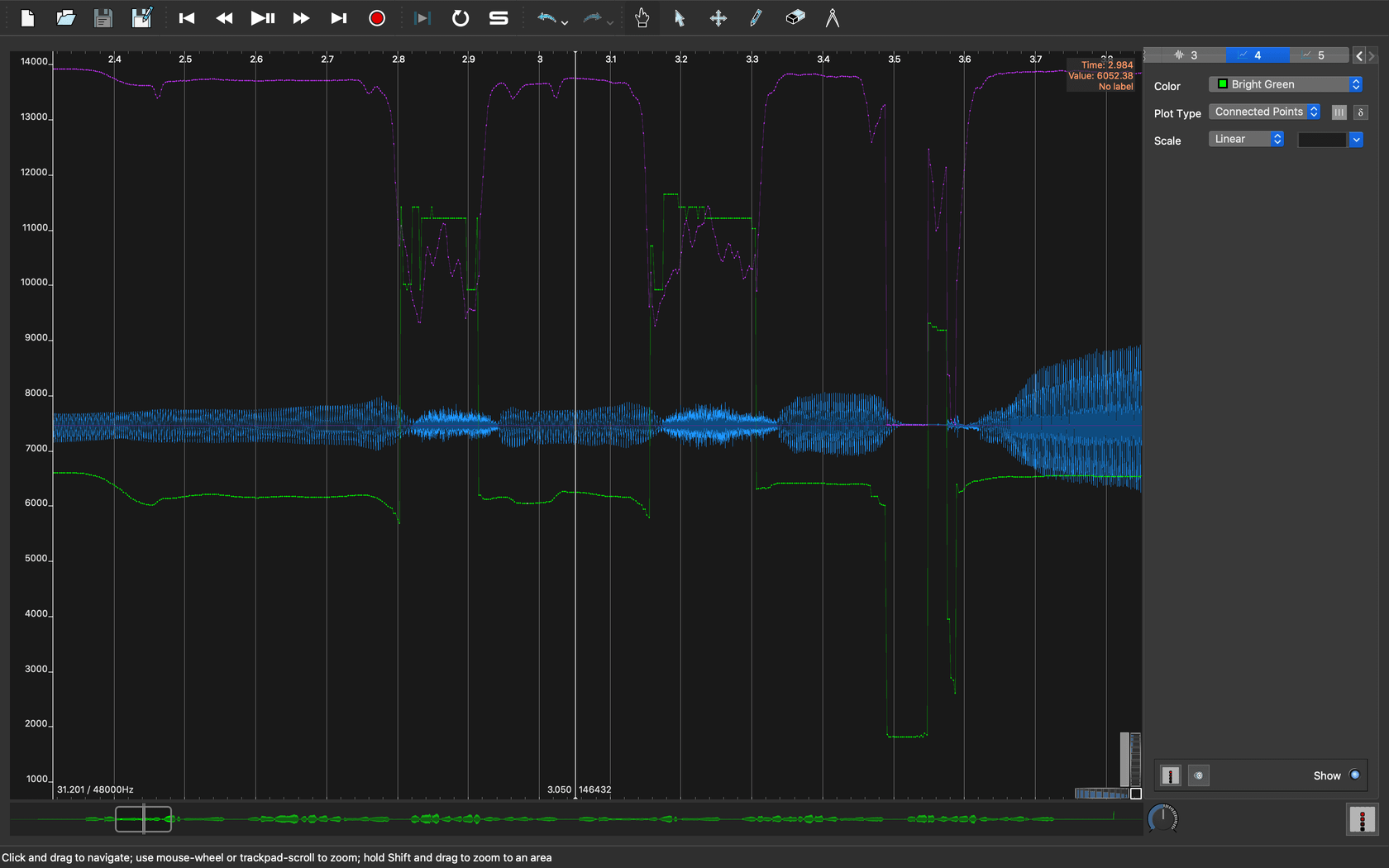図5. 歯擦音のピッチ信頼度の改善

歯擦音のピッチ信頼度が、周囲の母音部分と比べて大きく下がっている事がわかります。窓サイズ未指定時（デフォルト512サンプル）の時と比べると、周囲の母音部分とのピッチ信頼度の高低関係が逆転しています。これでピッチ信頼度の低い部分を「ピッチ無し（無声音）」と判定できそうです。

次に、13.5秒付近の母音ロングトーンのオクターブミスがどうなったのかをみてみます。


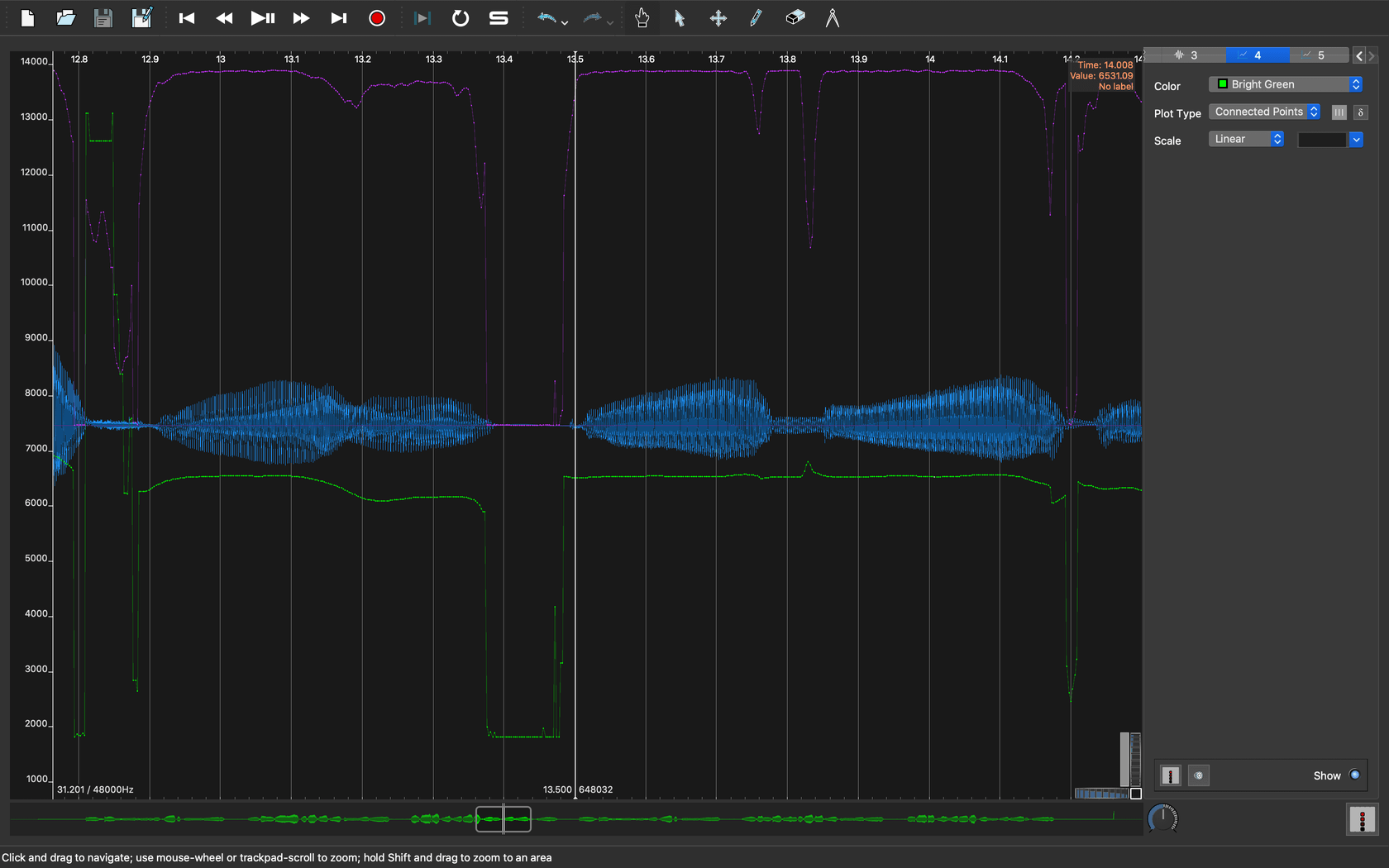図6. オクターブミスの改善

オクターブミスが完全に消えました。また、ピッチ信頼度も母音部分は比較的高く、無声化した区間では低く出ているため、ここでもピッチ信頼度の低い区間を「ピッチ無し（無声音）」と判定できそうです。

窓サイズ変更でなぜ推定結果が改善したのか

今回実験に用いたWAVEファイルのサンプリング周波数は48kHzです。これに対してデフォルトの窓サイズ512サンプルだと、最長でも $\frac{512}{48000} \fallingdotseq 10.6 ミリ秒$ の周期長しか扱えません。周波数に直すと最低93.75Hzの周波数までしか捉える事ができません。これは、本来低域側が持っているエネルギーが高域側に按分されてしまい、高域側のエネルギーが大きめに見積もられてしまう事を意味します。

また、窓長が短すぎて周波数分解能が悪いことも、ピッチ誤推定やオクターブミスの原因になっています。

おまけ

せっかくなので100セント単位で量子化したセント値もグラフに表示してみます。


図7. 100セント刻みのピッチ推定結果

緑の線に重なる形で表示している橙色の線が100セント刻みのピッチ推定値です。13.2秒付近を見ると階段状になっていることがわかります。なぜ100セント刻みなのかというと、100セントが丁度ピアノの鍵盤一つ分（半音）の間隔になっているので、この結果をピアノロールに対応づけるという応用目的のためです。

例えば自分の鼻歌をピッチ推定器にかけて100セント刻みで量子化すれば、ピアノロール化可能なデータを作れると言うことです。

おわりに

今回はこれまでのピッチ推定に関する要素技術のまとめとして、実際にツールとして動かせるピッチ推定器を作り、実際に動かしてみる実験をしました。また、性能を改善するための比較実験と考察も行っています。

ある意味で集大成のような内容に感じられるかもしれませんが、ここが音声信号処理におけるピッチ推定の出発点です。基礎的内容からやっと人間にとって意味のある応用分野への第一歩を踏み出した、と言ったところだと思います。

今後の発展としては、有声区間と無声区間の弁別処理をしてみたり、自己相関関数を求める際のゼロ値連結を2倍ではなく4倍や8倍にしてピッチ推定の性能が向上するか等を実験してみると楽しいかもしれません。窓サイズにしても、今はわかりやすさのためにサンプル数指定ですが、WAVEファイルのサンプリング周波数に応じて長さを固定化したいとなると秒指定が良いと思います。

また、今回は窓関数をブラックマンハリスで固定化していましたが、別の窓関数に差し替えたり、窓関数を変えて複数回処理した結果から妥当なピッチを推定すると言った、もう少し複雑なアルゴリズムに挑戦してみるのも良いでしょう。

ちなみに、ゼロ値連結した自己相関関数を使ってピッチ推定する手法については大分昔に論文が出ていたはずなので、見つけたら参考文献として載せようと思います。

ピッチ推定ツールを作る