はじめに

DFTで周波数変換する際に窓関数の概念は避けて通れません。今まで窓関数を使った事がないという方の場合、それは矩形窓を使っていた事になります。

矩形窓は窓幅いっぱいに1が並んだだけの窓なので、対象信号に何も変更を加えません。そのため、「矩形窓を使っている」と言われても、何か屁理屈のように感じられるかもしれません。

しかし、窓関数が周波数領域でどのような意味を持つかを理解すると、なぜ対象信号に何も施さずにDFTで周波数変換するときに「矩形窓をかけた」と解釈するのか、納得できると思います。

畳み込みの定理

畳み込みの定理とは離散フーリエ変換（DFT）で周波数変換する際の、原信号側の積と周波数領域側での畳み込み積分が等しいとする定理です。
また、その逆で、原信号側の畳み込み積分は、周波数領域側での積になります。

\begin{aligned}
原信号での各点同士の&積&=&周波数領域での周波数成分同士の畳み込み積分
\end{aligned}

\begin{aligned}
原信号での各点同士の&畳み込み積分 &=&周波数領域での周波数成分同士の積
\end{aligned}

原信号での積の代表例は、DFTの文脈における窓関数掛けです。原信号をN点取り出し、それぞれに係数を掛けるのが窓関数掛けあるいは単に窓がけと呼ばれる処理です。

窓をかけた信号の周波数成分は、窓関数と原信号をそれぞれDFTし、そのスペクトラム同士で畳み込み積分を求めた結果と等しくなります。

逆に、スペクトラムに窓関数を掛けた結果は、窓関数をIDFTし、原信号と畳み込み積分を求め、DFTで周波数変換した結果と等しくなります。

窓関数の周波数特性

窓関数をDFTで周波数変換すると。窓関数の周波数特性がわかります。試しにハン窓（hann window）の周波数特性を見てみます。

import numpy
import scipy.signal
import scipy.fftpackh
import matplotlib.pyplot as plt
import sys

window = scipy.signal.hann(512)
spectrum = numpy.abs(scipy.fftpack.fft(window)) / len(window)
spectrum_db = 20 * numpy.log10(spectrum + sys.float_info.min)
spectrum_db = numpy.r_[spectrum_db[len(spectrum_db)//2:], spectrum_db[:len(spectrum_db)//2]]
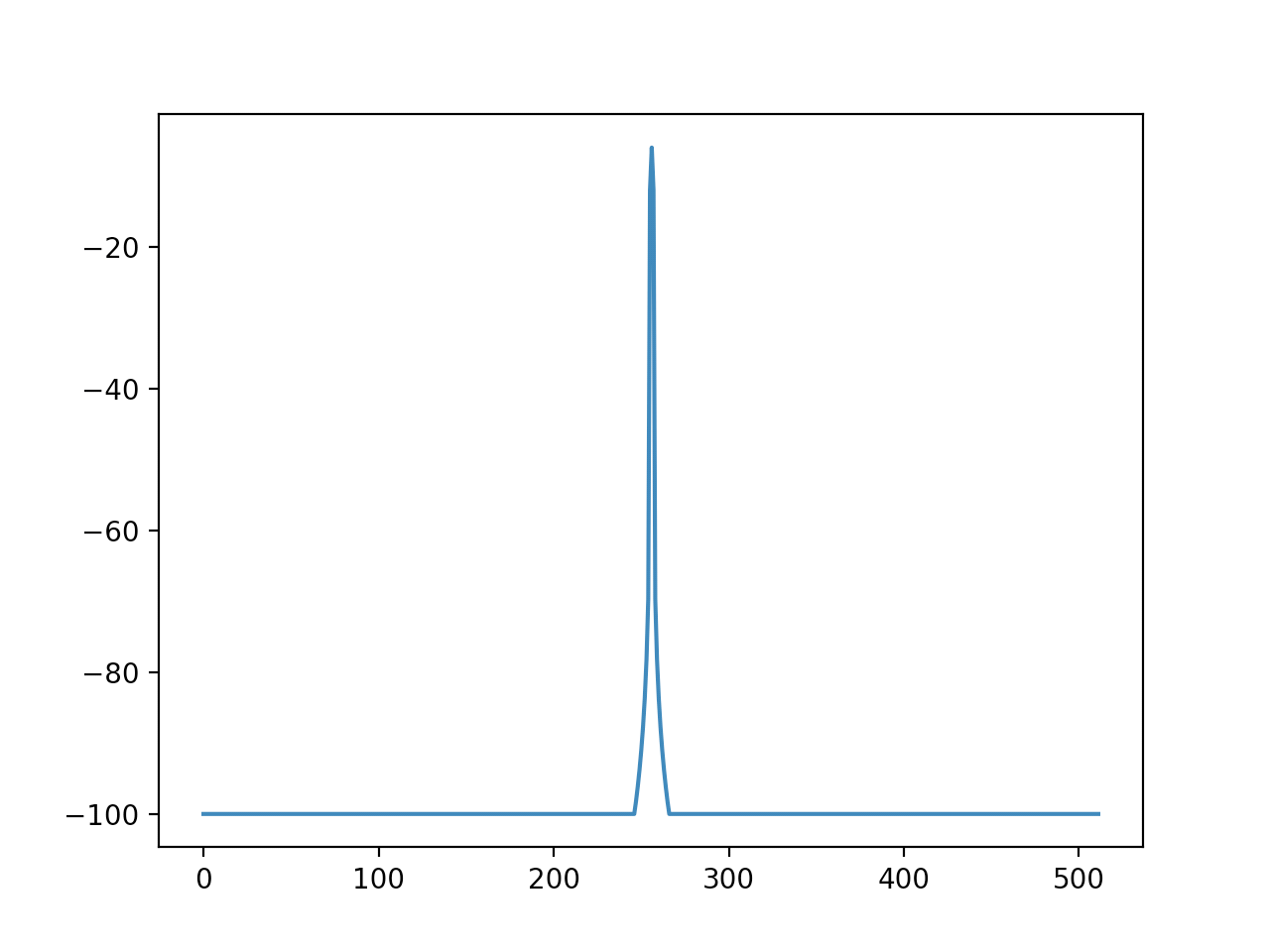
plt.plot(numpy.clip(spectrum_db, -100, 0))
plt.show()

振幅スペクトラムは線対称になっており、窓関数のいわゆるメインローブ部分が0 bin目なので、スペクトラム配列の前半と後半を入れ替えています。
このままだと「ふーん」という感じですが、窓関数の前後にゼロ値を追加して周波数分解能をあげるとどうなるでしょうか？

import numpy
import scipy.signal
import scipy.fftpack
import matplotlib.pyplot as plt
import sys

ws = 512
zs = 4096
ps = (zs - ws) // 2

window = numpy.r_[numpy.zeros(ps), scipy.signal.hann(ws), numpy.zeros(ps)]

spectrum = numpy.abs(scipy.fftpack.fft(window)) / len(window)
spectrum_db = 20 * numpy.log10(spectrum + sys.float_info.min)
spectrum_db = numpy.r_[spectrum_db[len(spectrum_db)//2:], spectrum_db[:len(spectrum_db)//2]]
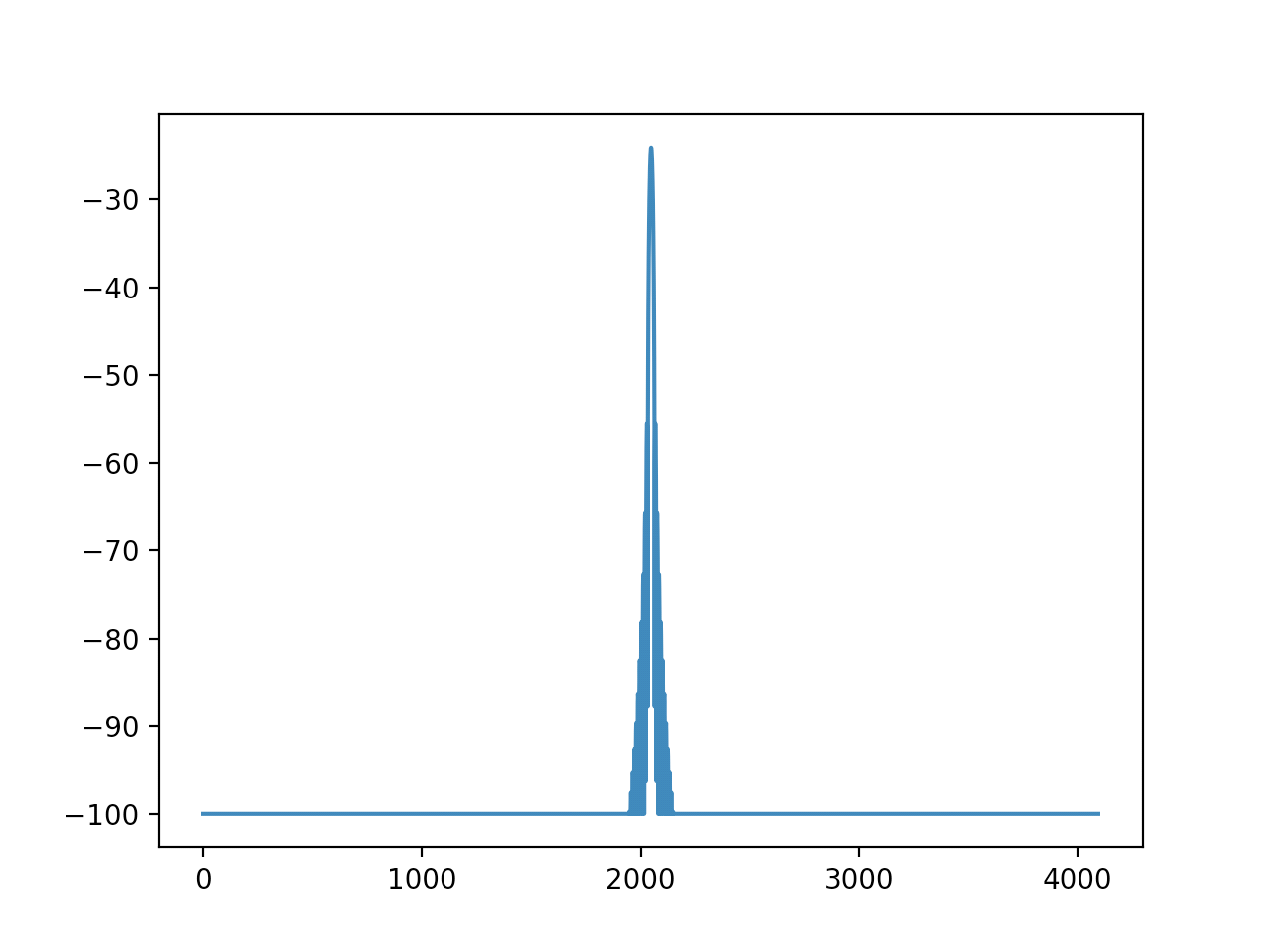
plt.plot(numpy.clip(spectrum_db, -100, 0))
plt.show()

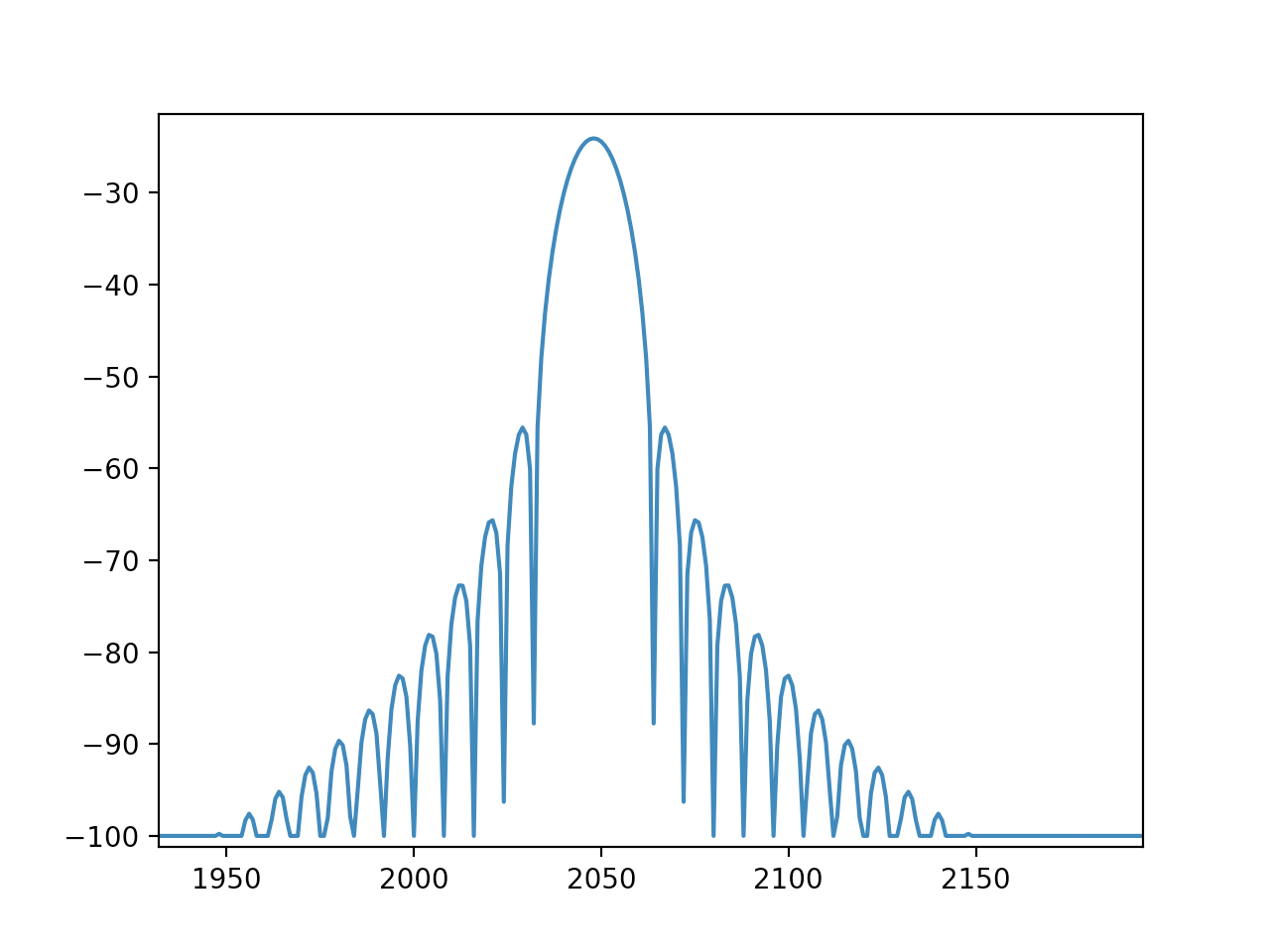
窓長通りでDFTすると、正規化整数周波数binの成分のみが出てくるため、なだらかな特性に見えますが、窓関数の前後にゼロ値を追加してDFTの窓長を長くし、周波数分解能をあげると、正規化整数周波数binの間にも成分が存在していることがわかります。

要はこのスペクトル配列を、原信号のスペクトラムへ畳み込むのが、原信号に窓関数をかける事の意味です。

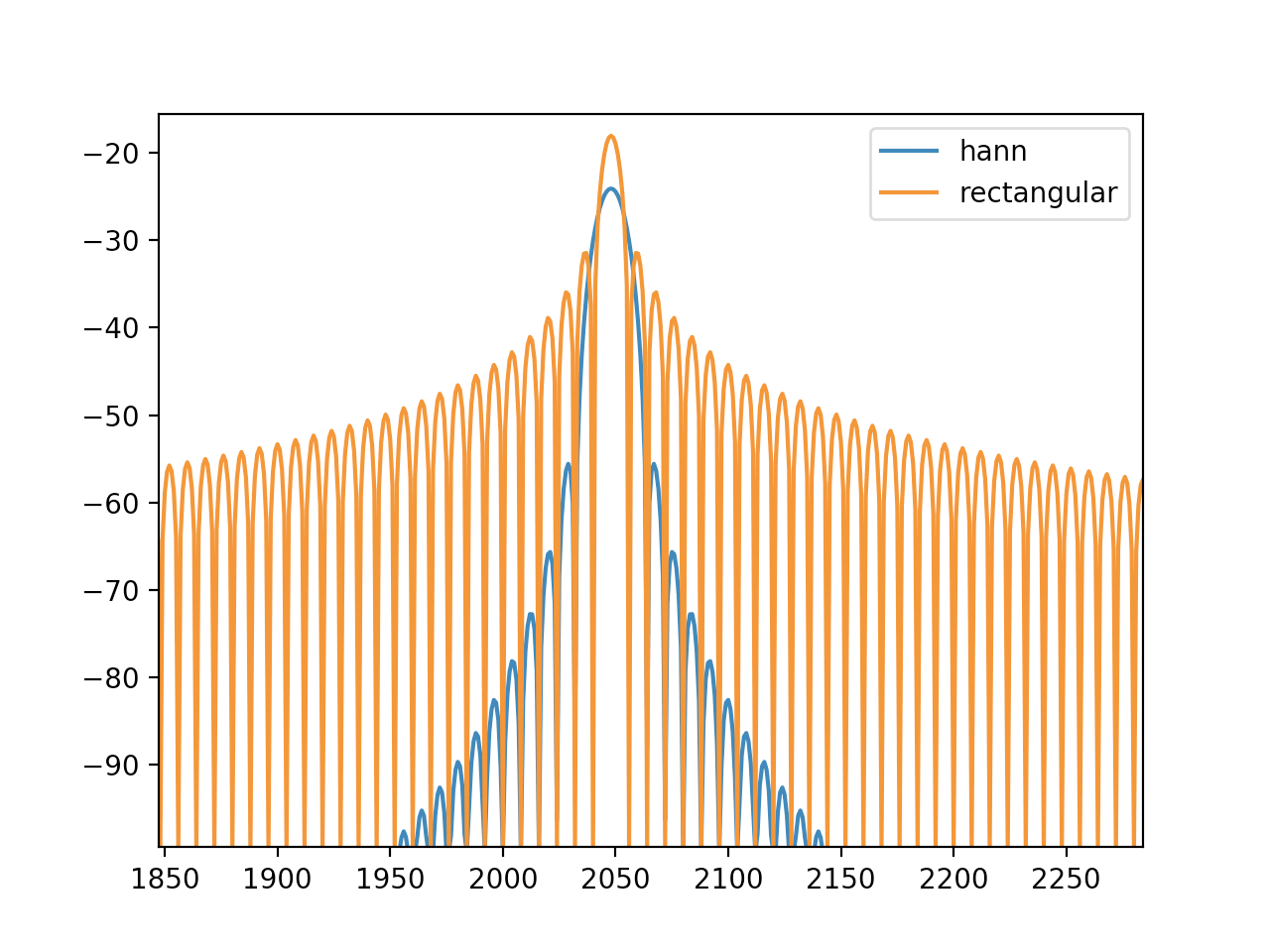
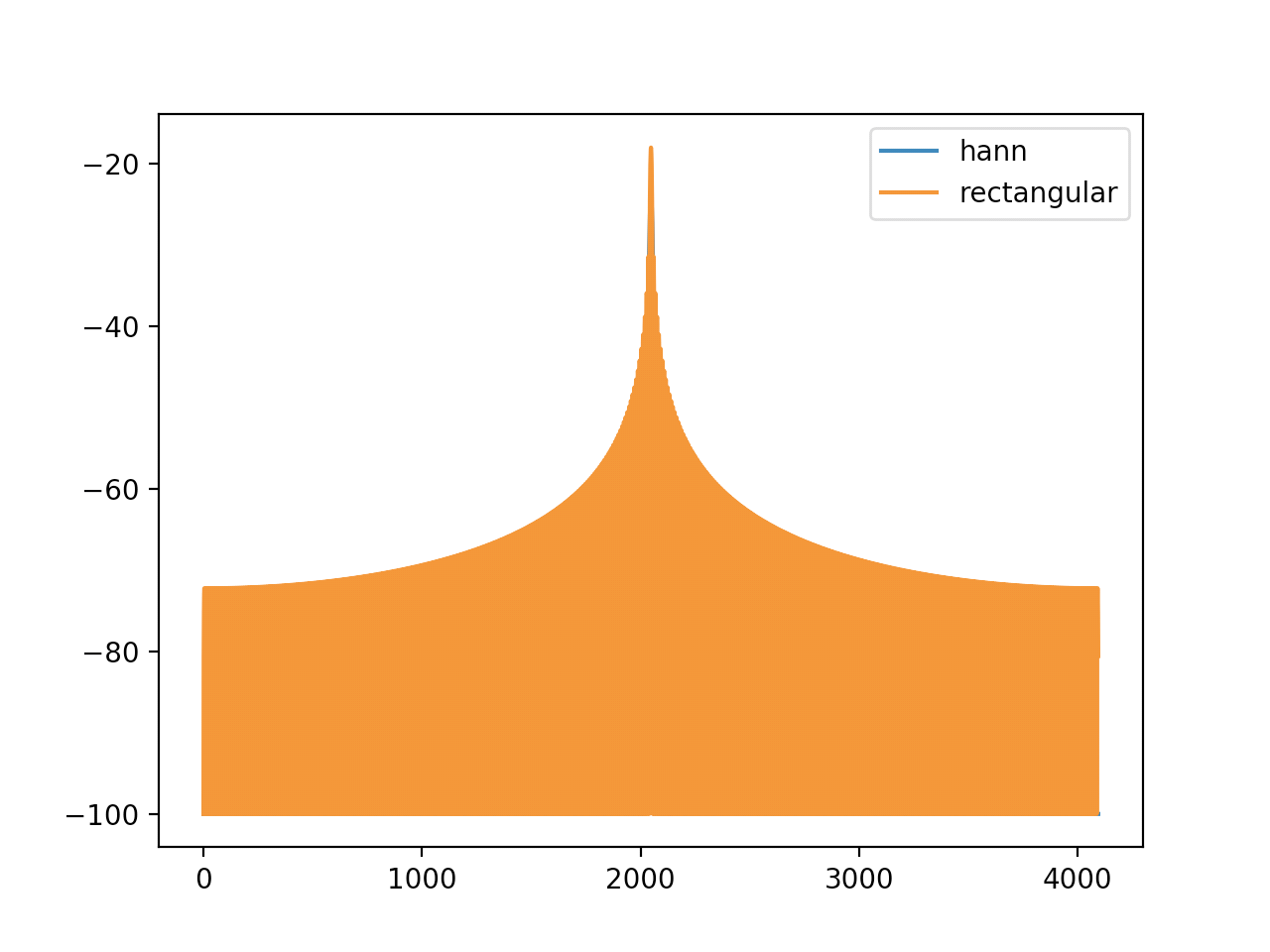
折角なので矩形窓の特性も見て、ハン窓と比べてみましょう。

import numpy
import scipy.signal
import scipy.fftpack
import matplotlib.pyplot as plt
import sys

def __make_window_spectrum(window, size):
    ws = len(window)
    ps = (size - ws) // 2
    window = numpy.r_[numpy.zeros(ps), window, numpy.zeros(ps)]
    spectrum = numpy.abs(scipy.fftpack.fft(window)) / len(window)
    spectrum_db = 20 * numpy.log10(spectrum + sys.float_info.min)
    ws_half = len(spectrum_db)//2
    spectrum_db = numpy.r_[spectrum_db[ws_half:], spectrum_db[:ws_half]]
    return spectrum_db

hann_spectrum = __make_window_spectrum(scipy.signal.hann(512), 4096)
rect_spectrum = __make_window_spectrum(scipy.signal.boxcar(512), 4096)

plt.plot(numpy.clip(hann_spectrum, -100, 0), label="hann")
plt.plot(numpy.clip(rect_spectrum, -100, 0), label="rectangular")
plt.legend()
plt.show()

矩形窓の方は裾野が広いので、これを原信号のスペクトラムに畳み込むと、実際にはエネルギーが無い周波数binに、他の周波数binのエネルギーが流れ込んできます。

矩形窓、つまりDFT時に原信号に何もかけない、という選択はつまり、このような裾野の広いフィルタカーネルで、原信号スペクトラムを畳み込んでいる事になるのです。

周波数分析の目的によっては、矩形窓はあまり良い性能を発揮しないため、色々な窓関数を試す事になります。色々試す場合にも、この畳み込みの定理を把握しておけば、どういった周波数特性の窓関数が必要なのか、ある程度方針を立てることもできますし、その気になれば、分析の目的に適した窓関数を自作することもできるようになります。

畳み込み積分の高速化

畳み込み積分はご存知の通り非常に計算量が多いです。自分自身との畳み込み積分ともなれば、O(N^2)の計算量になります。
一方、信号に対する掛け算は、信号長をNとすればO(N)、DFTはNが2のべき乗の時、効率的な計算方法であるFFTが知られており、その計算量はO(N * log(N))です。

O(N^2)とO(N + 2N * log(N))の比較なので、8 \leqq Nの場合は窓掛けしてDFTで変換した方が計算量は少なくなります。

自分自身との畳み込み積分

再三の説明ですが、周波数領域における積は、元の信号領域における畳み込み積分になります。

では、原信号をDFTで周波数成分した後、その周波数成分を自乗（二乗）した場合はどうなるでしょうか？自分自身と同じ成分で積を計算している事になるので、原信号領域では自分自身との畳み込み積分になるはずです。つまり、自己相関関数になります。

自己相関関数とパワースペクトラム

周波数成分の自乗とはつまりパワースペクトラムの事で、パワースペクトラムに変換するということはつまり、原信号領域における自己相関関数を求めている事と（表現は違えど）ほぼ同じだという事ですね。

おわりに

畳み込みの定理は応用が効く考え方です。窓関数の自作や理想的な周波数特性を持つFIRフィルタの設計（窓関数法）といった応用の他、近年ではインパルスレスポンスリバーブの高速化や、ニューラルネットワークの畳み込み層の高速化等にも応用されています。

工学の様々な場面で登場する積や畳み込み積分を、畳み込みの定理の側面から解釈することで、何か新しい発見があるかもしれませんね。