前回のあらすじと本記事の概要 FIRフィルタを行列表現すると巡回行列になりました。その巡回行列をさらに分解すると巡回置換行列で表現できる事がわかりました。本記事ではさらに巡回置換行列の性質を考えてみます。 前置き:特殊な
Read more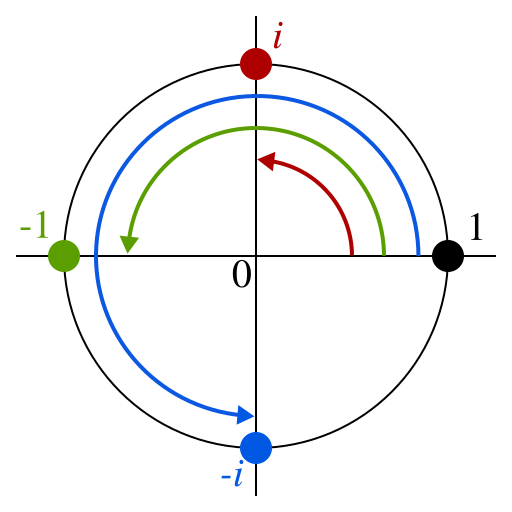
信号処理を勉強する

前回のあらすじと本記事の概要 FIRフィルタを行列表現すると巡回行列になりました。その巡回行列をさらに分解すると巡回置換行列で表現できる事がわかりました。本記事ではさらに巡回置換行列の性質を考えてみます。 前置き:特殊な
Read more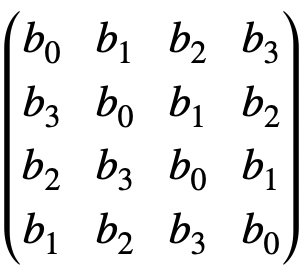
はじめに FIRフィルタは畳み込み積分とよく言われますが、そもそも畳み込み積分と言われてもそれがなんなのかよくわかりません。そこで、身近な線形代数の知識を使ってFIRフィルタを行列で表現し、その特性を調べてみます。 FI
Read more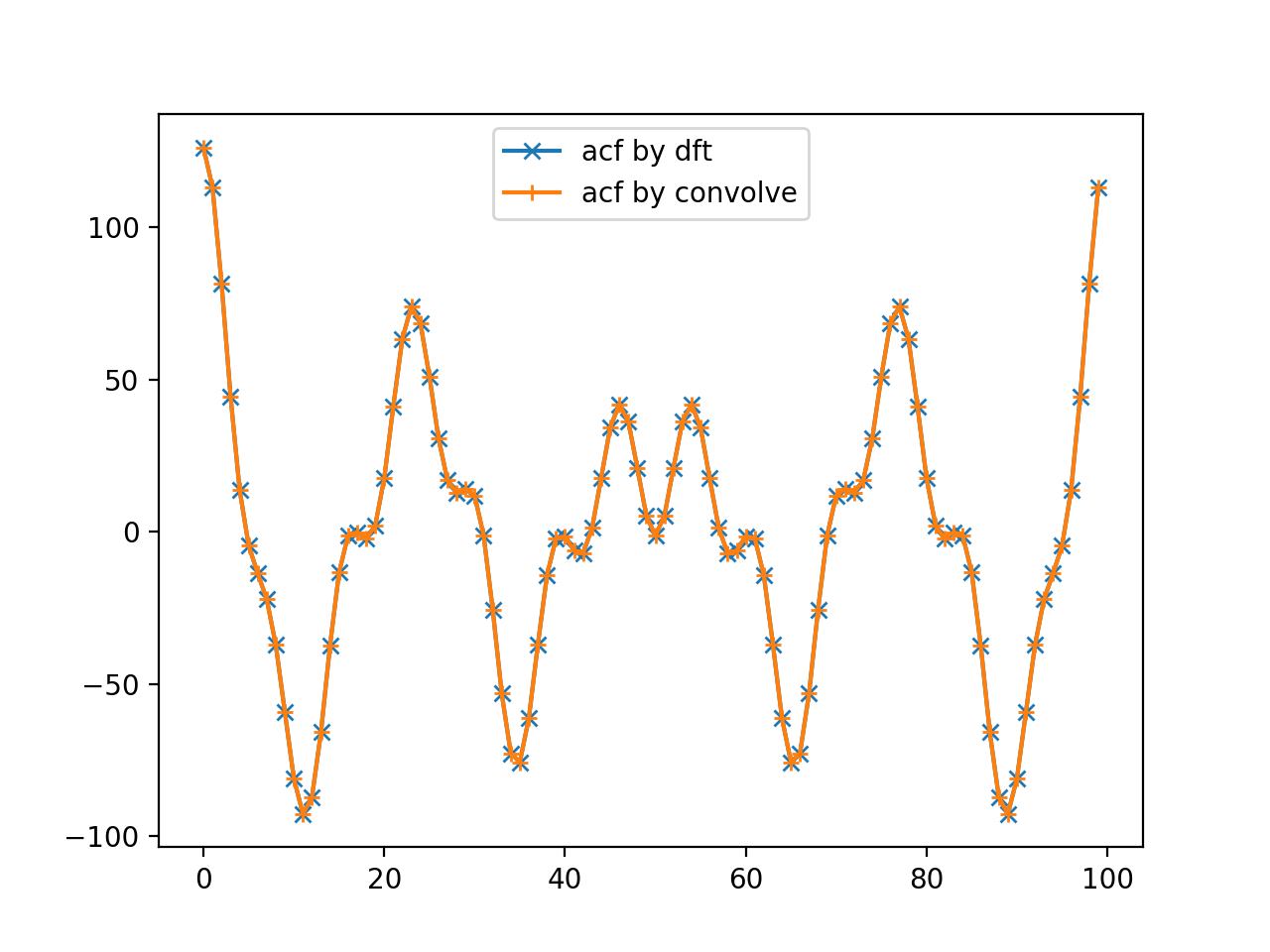
信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。
Read more
はじめに ものの本にはあまりはっきりと書かれていなかったりしますが、線形代数を学習すると、離散フーリエ変換(DFT)は三角関数によって構成された直交基底を用いた直交変換だということがわかります。 ここでは、三角関数で直交
Read more