自己相関関数とパワースペクトラム

信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。

ACF(\tau) = \sum_{i=0}^{N-1} x_i x_{i-\tau}

\tauは時間の遅れを表す値なので、この式は、過去にさかのぼりながら現在の信号と過去の信号との間で内積を求めていく式です。計算自体はいわゆる畳み込み積分です。
無限長の信号であれば、延々と過去にさかのぼることができますが、ここでは信号長がNなので、過去の信号もx_0からx_Nの繰り返しとします。
そうすると、\tauの値も0からN-1となります。つまり、元の信号長Nに対して、ACFもN個の値になります。
pythonコードで表現すると以下の通りです。

def acf_by_convolve(values):
    repeated = numpy.r_[values, values]
    N = len(values)
    acf = numpy.zeros(N)
    for i in range(len(values)):
        acf[i] = numpy.dot(values, repeated[N - i:N * 2 - i])
    return acf

ひとまず定義通りに過去方向にスライドさせながら内積を計算しています。
未来方向にスライドさせながら内積を計算しても、実は同じ結果になります。

巡回離散信号の自己相関関数は、離散フーリエ変換と離散逆フーリエ変換を使って計算することもできます。

ACF(\tau) = real(IDFT((abs(DFT(x)))^{2}))

pythonコードで表現すると以下の通りです。

def acf_by_dft(values):
    power_spectrum = numpy.abs(scipy.fftpack.fft(values)) ** 2
    return numpy.real(scipy.fftpack.ifft(power_spectrum))

DFTで求めた振幅スペクトラムを二乗し、その値をIDFTでまた時間信号に戻しています。
振幅スペクトラムだけを使っているので、位相はゼロです。

畳み込み積分定義とDFT定義の結果が同じになるか見てみます。

import sys
import numpy
import scipy.fftpack
import matplotlib.pyplot as plt

def sin_wave(length, frequency):
    angles = numpy.linspace(0, numpy.pi * 2 * frequency, length)
    return numpy.sin(angles)

def multi_sin_wave(length, frequency_array, amplitude_array):
    wave = numpy.zeros(length)
    for frequency, amplitude in zip(frequency_array, amplitude_array):
        wave += sin_wave(length, frequency) * amplitude
    return wave

if __name__ == "__main__":
    N = 100

    cyclic_data = multi_sin_wave(
        N,
        [2.0, 4.0, 5.0, 7.0, 7.5, 10.0, 13.0],
        [0.2, 1.0, 0.8, 0.5, 0.3,  0.2,  0.7])

    acf_a = acf_by_dft(cyclic_data)
    acf_b = acf_by_convolve(cyclic_data)

    plt.plot(cyclic_data, label="cyclic data")
    plt.legend()
    plt.show()

    plt.plot(acf_a, label="acf by dft", marker="x")
    plt.plot(acf_b, label="acf by convolve", marker="+")
    plt.legend()
    plt.show()

    sys.exit(0)

multi_sin_wave()で複数のsin波形を足し合わせた信号を生成しています。
以下の様な信号を生成しました。

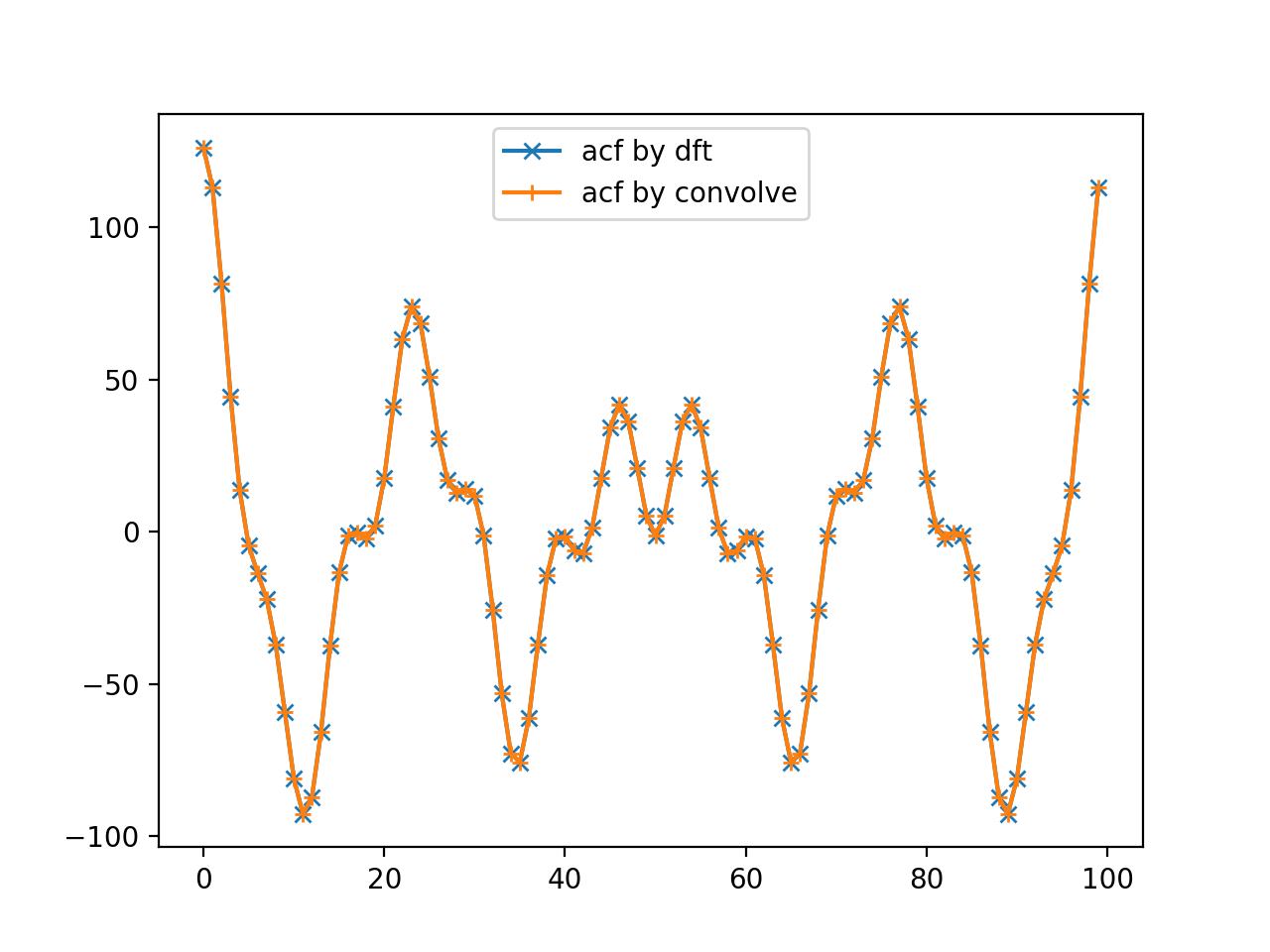
この信号に対してそれぞれの方法で自己相関関数を計算した結果です。

結果を見ると、畳み込み積分による計算結果もDFTによる計算結果も一致していることがわかります。

自己相関関数は、同じ様な信号パターンの時に値が高くなります。
内積を計算しているので、相互相関係数の様な値を計算していることになります。
0が無相関、直交を意味し、正負に大きくなるほど相関が大きくなります。

自己相関関数を相関係数列に変換する場合には、acf_a[全体をacf_a[0]で割ることで、値を-1から1の間にスケーリングすることができます。値を-1から1にスケーリングした方が、原信号のエネルギーに依存せず、より抽象化された構造情報が得られるため、閾値処理等を施しやすくなります。