前回のあらすじと本記事の概要 FIRフィルタを行列表現すると巡回行列になりました。その巡回行列をさらに分解すると巡回置換行列で表現できる事がわかりました。本記事ではさらに巡回置換行列の性質を考えてみます。 前置き:特殊な
Read more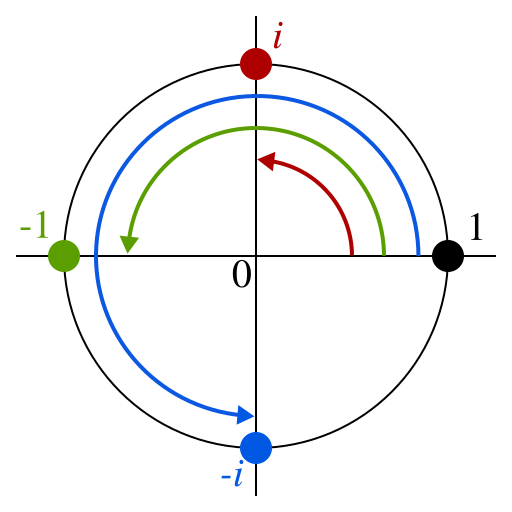
信号処理を勉強する

前回のあらすじと本記事の概要 FIRフィルタを行列表現すると巡回行列になりました。その巡回行列をさらに分解すると巡回置換行列で表現できる事がわかりました。本記事ではさらに巡回置換行列の性質を考えてみます。 前置き:特殊な
Read more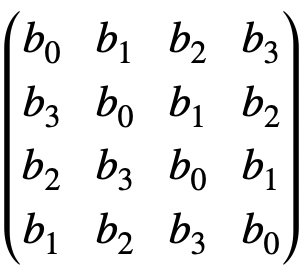
はじめに FIRフィルタは畳み込み積分とよく言われますが、そもそも畳み込み積分と言われてもそれがなんなのかよくわかりません。そこで、身近な線形代数の知識を使ってFIRフィルタを行列で表現し、その特性を調べてみます。 FI
Read moreはじめに FIRフィルタは畳み込み積分で実現するフィルタです。そのまま計算する場合、処理は非常にシンプルですが、計算量も非常に多く、フィルタカーネル長が長くなればなるほど非現実的な処理時間になってしまいます。この問題に対
Read moreはじめに 信号処理の理論ばかり追っていてもどう役に立てれば良いのかわからず、なかなかモチベーションが上がりません。 今回は、信号処理の応用例として、人間の声のピッチ、つまり音程を自己相関関数で推定してみます。
Read more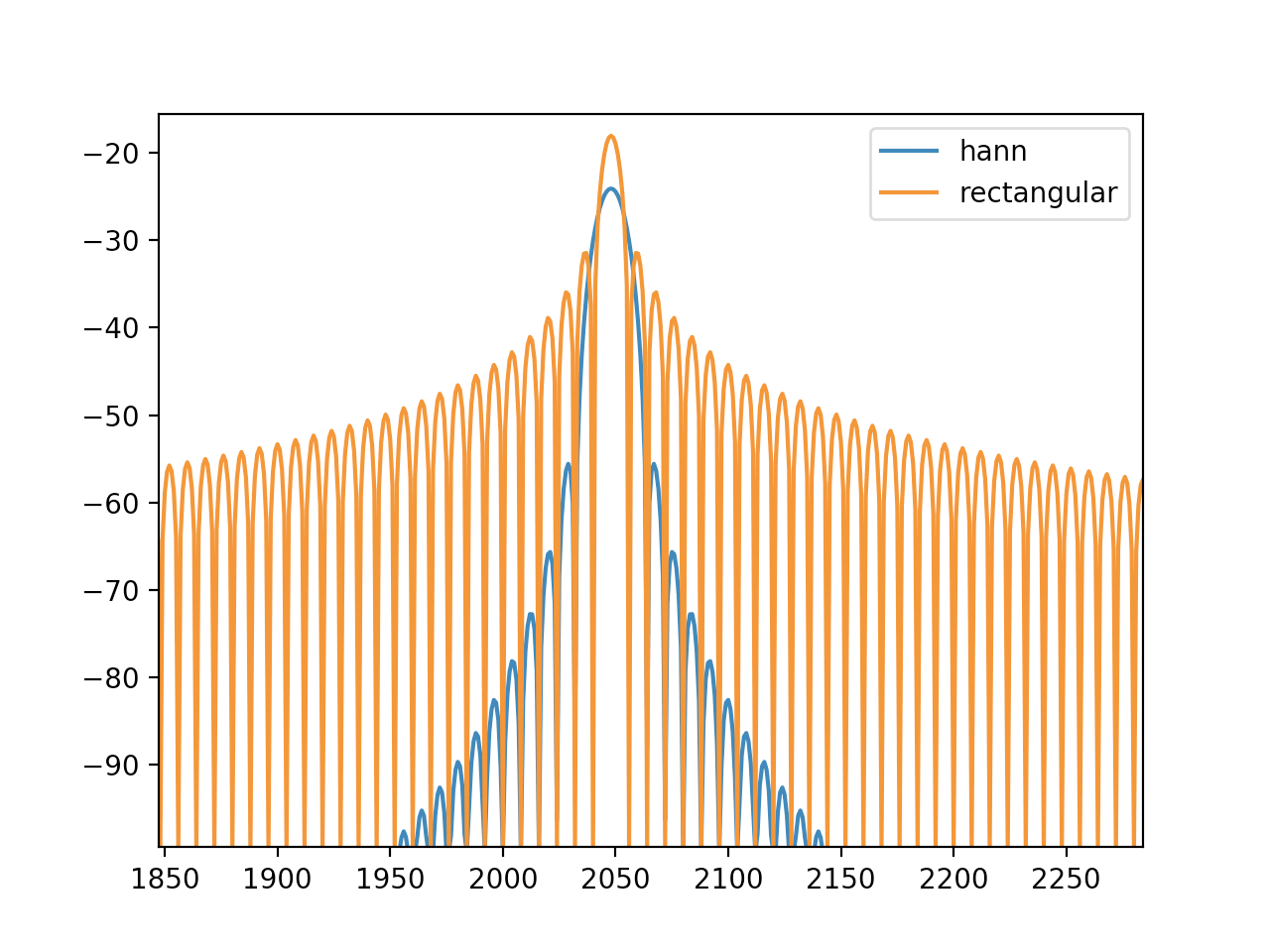
はじめに DFTで周波数変換する際に窓関数の概念は避けて通れません。今まで窓関数を使った事がないという方の場合、それは矩形窓を使っていた事になります。
Read more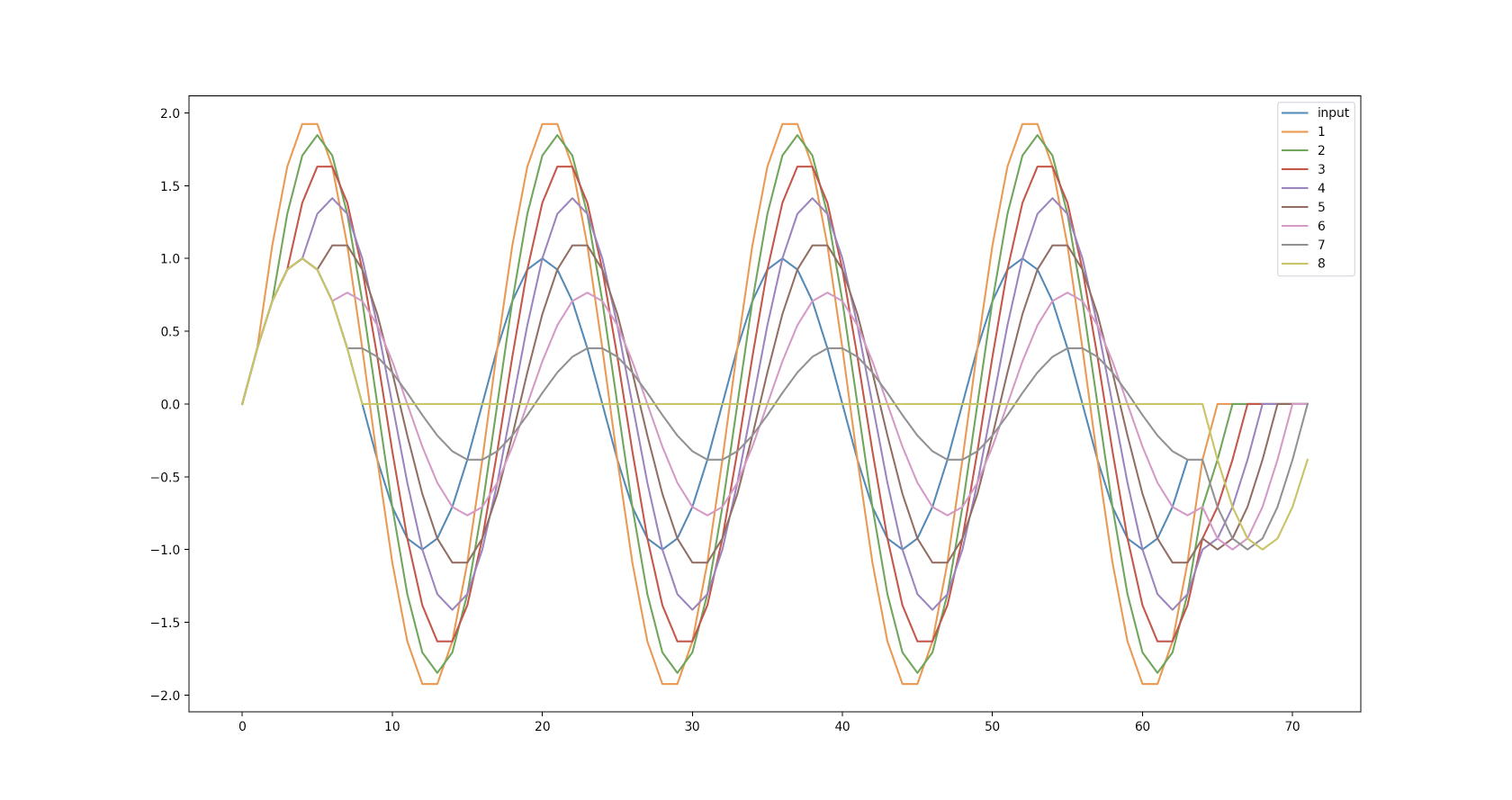
はじめに 信号処理といえばフィルタは欠かせない概念です。音声や画像といったみじかな情報に対して施されるものから、電波通信の周波数変調、信号波の取り出し、はたまた統計処理等の様々な工学分野で応用されています。 数学にもフィ
Read more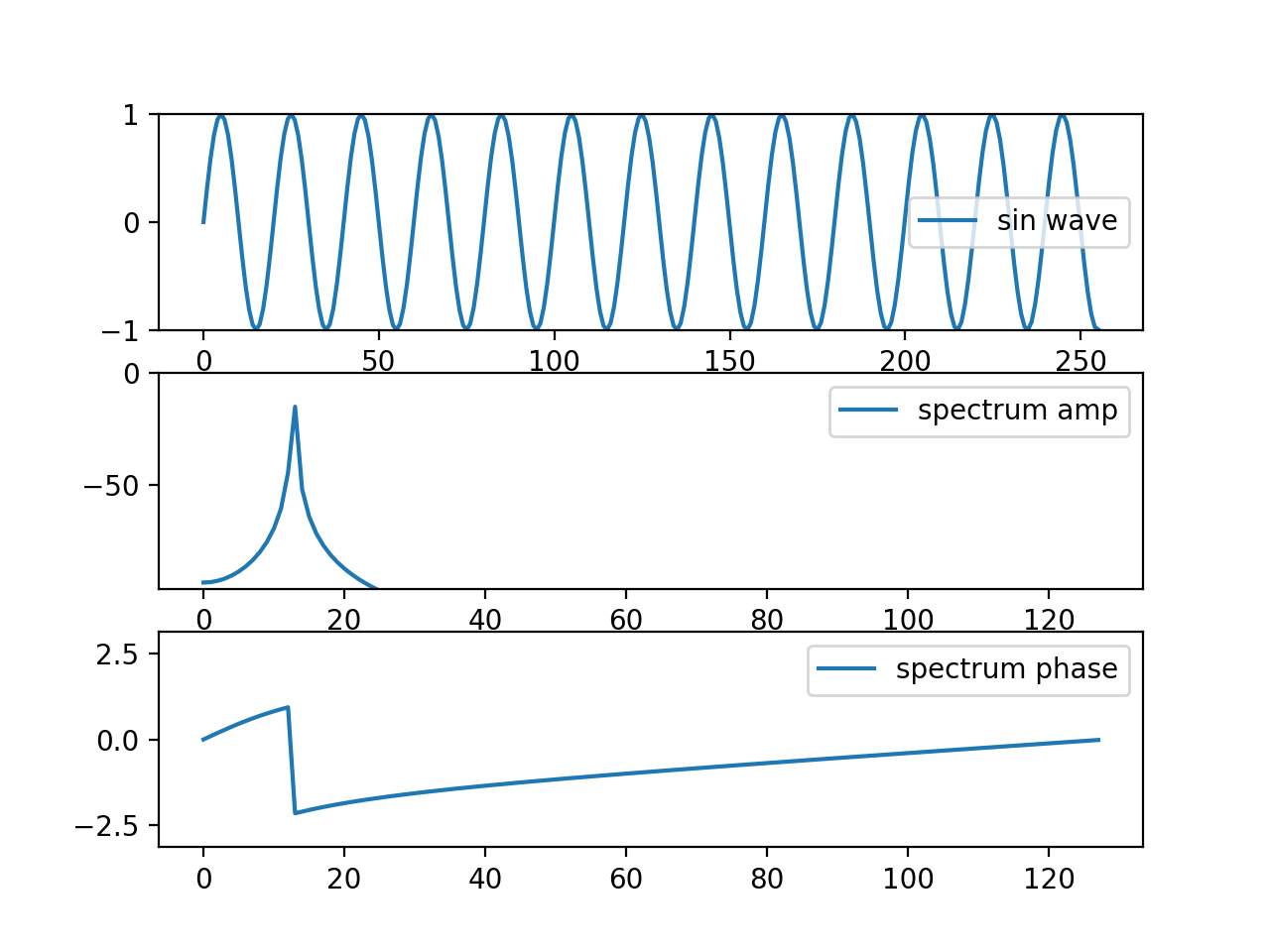
離散フーリエ変換は、窓長を1周期とする周期性のある波を最長とし、その整数倍周波数の足し合わせ表現に原信号を変換します。原信号が素直に整数倍の周波数のサイン波で構成されていれば、いわゆるサイドローブが現れず、綺麗な変換結果
Read more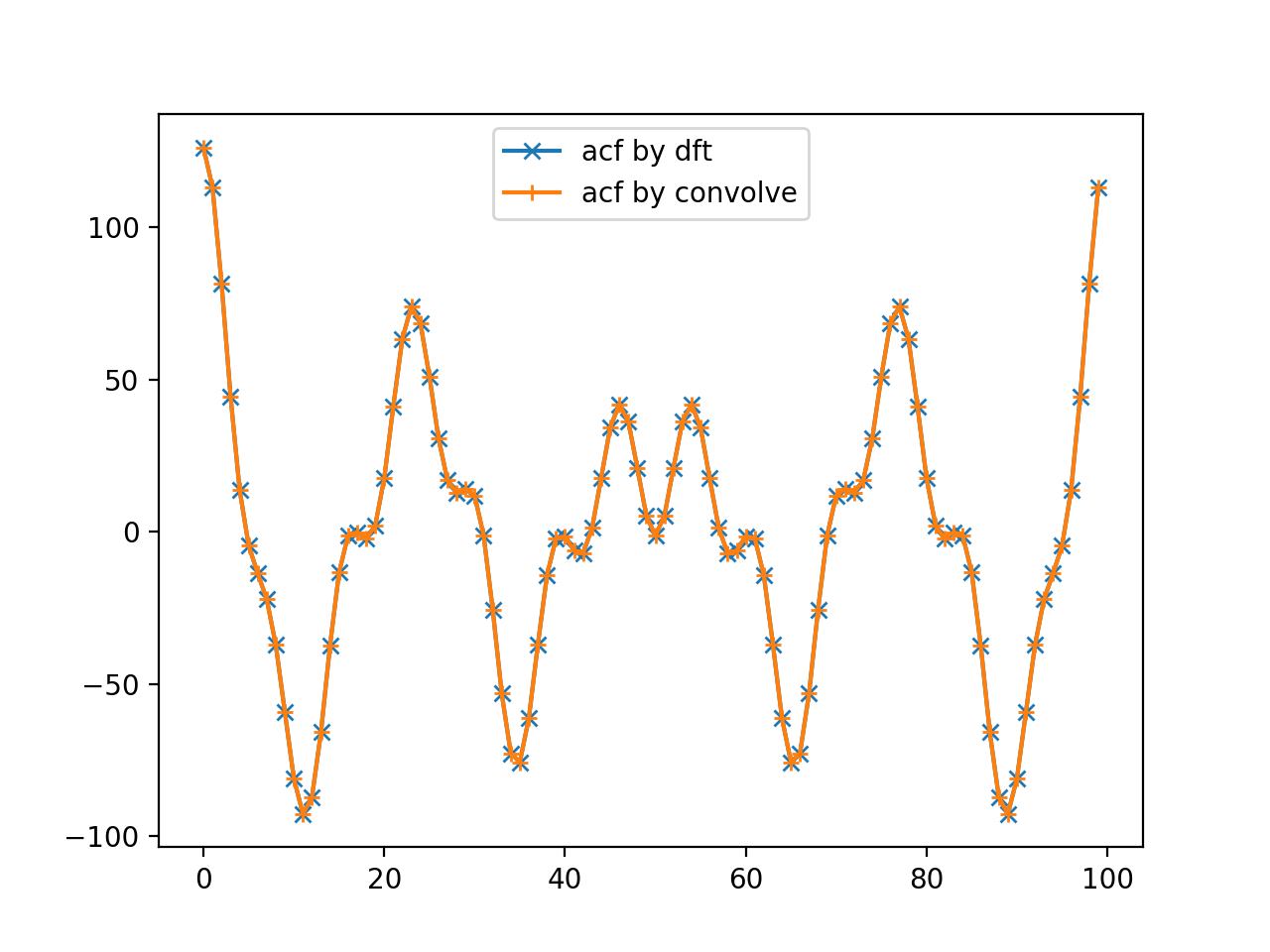
信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。
Read more