はじめに
信号処理といえばフィルタは欠かせない概念です。音声や画像といったみじかな情報に対して施されるものから、電波通信の周波数変調、信号波の取り出し、はたまた統計処理等の様々な工学分野で応用されています。
数学にもフィルタ理論というものが存在するようですが、難しすぎてよくわかりません。
そもそもフィルタっていうのが何なのかですが、コーヒーフィルタやエアコンフィルタのように、利用者にとって望ましいものを通し、望ましくないものを通さない機能を持つ仕組みの事をフィルタと呼びます。
信号処理においても概ねそのような性質を持つ仕組みの事をフィルタと呼びます。
線形時不変システム
信号処理の本(すごく古い本)等を読んでいると、突然線形時不変システムなる言葉が出てくる事があります。
線形とはそのシステムが線形性を持つ事、つまり、四則演算について、分配法則や結合法則といった法則が成り立つ事を意味します。
時不変とは、システムの性質が時間に依存して変化したりしない、という事を意味します。
この線形時不変システムは、そうではないシステムと比べて数学的には非常に扱いやすい性質を持っていることがわかっています。また、その表現力、応用範囲も広く、有用であるため、まずは線形時不変システムを学ぶだけでも実用性があります。
ここでシステムと言うのは、何かしらの入力を受けて、何かしらの出力を出すブラックボックスの事です。現実には、プログラムだったり電気回路だったりします。
FIRフィルタ
線形時不変システムの中でもさらに狭い範囲のシステムとして、FIRフィルタ(有限インパルス応答フィルタ、finite impulse response filter)を考えます。
FIRフィルタの計算自体は非常に簡単です。信号列に対して、有限長のフィルタ係数列を畳み込むだけです。畳み込みとは、正式には畳み込み積分と呼ばれる演算の事で、二つの信号列(数列、範囲が任意の関数)同士を、スライドさせながら内積を求めていくだけです。
例えばPython+Numpyで、以下の通りに計算できます。
import numpy
signal = [1,2,3,4,5]
kernel = [1,-1]
convolved = numpy.convolve(signal, kernel)
上記のプログラムのnumpy.convolveは、signalに対して、位置をスライドさせながらkernelとの内積を計算し、その結果の配列を返します。
この畳み込み積分の計算は、FIRフィルタを施す事と等価です。
それでは、上記プログラムで施した畳み込み積分は、FIRフィルタとしてみた場合にどういう性質を持つでしょうか?
インパルス応答
便宜的に、ある瞬間の時刻にのみ1の強さ、それ以外の全ての時刻で0の強さの信号をインパルス信号と呼びます。
インパルス信号を線形時不変システムに入力すると何が出てくるかというと、その線形時不変システムをフィルタとしてみた場合のフィルタ係数列が出てきます。
線形時不変システムが完全にFIRフィルタだった場合、要は何かしらの係数列を入力信号に畳み込んでいるだけです。そのため、インパルス信号をFIRフィルタに入力すると、FIRフィルタの係数列がそのまま出てきます。
import numpy
impulse = [1,0,0,0,0,0,0,0,0,0,0]
kernel = [4,3,2,1,0,0]
numpy.convolve(impulse, kernel)
array([4, 3, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
出力結果の先頭部分にkernelで定義した値と同じ数列が出てきました。このように、謎のシステムにインパルス信号を入力し、その出力(応答)をとることで、ブラックボックスだったシステムの特性を解析することができますが、ここではこれ以上触れません。
ここでは、kernel=[1,-1]がFIRフィルタとしてみた場合にどういう性質を持つのか、ということが問題でしたので、先に進みます。
FIRフィルタのカーネルの性質
FIRフィルタの係数列の事をフィルタカーネルと呼びます。フィルタカーネルに対して、適当な数のゼロ値を連結して切りの良い個数の数列にしてしまい、DFTを施す事で周波数領域に変換します。
Python+Numpy+Scipyで簡単に周波数領域に変換できます。
import sys
import numpy
import scipy.fftpack
import matplotlib.pyplot as plt
kernel = numpy.r_[[1,-1], numpy.zeros(254)]
spectrum = 20 * numpy.log10(numpy.abs(scipy.fftpack.fft(kernel)) + sys.float_info.min)
plt.plot(numpy.clip(spectrum, -100, 20)[:128])
plt.show()
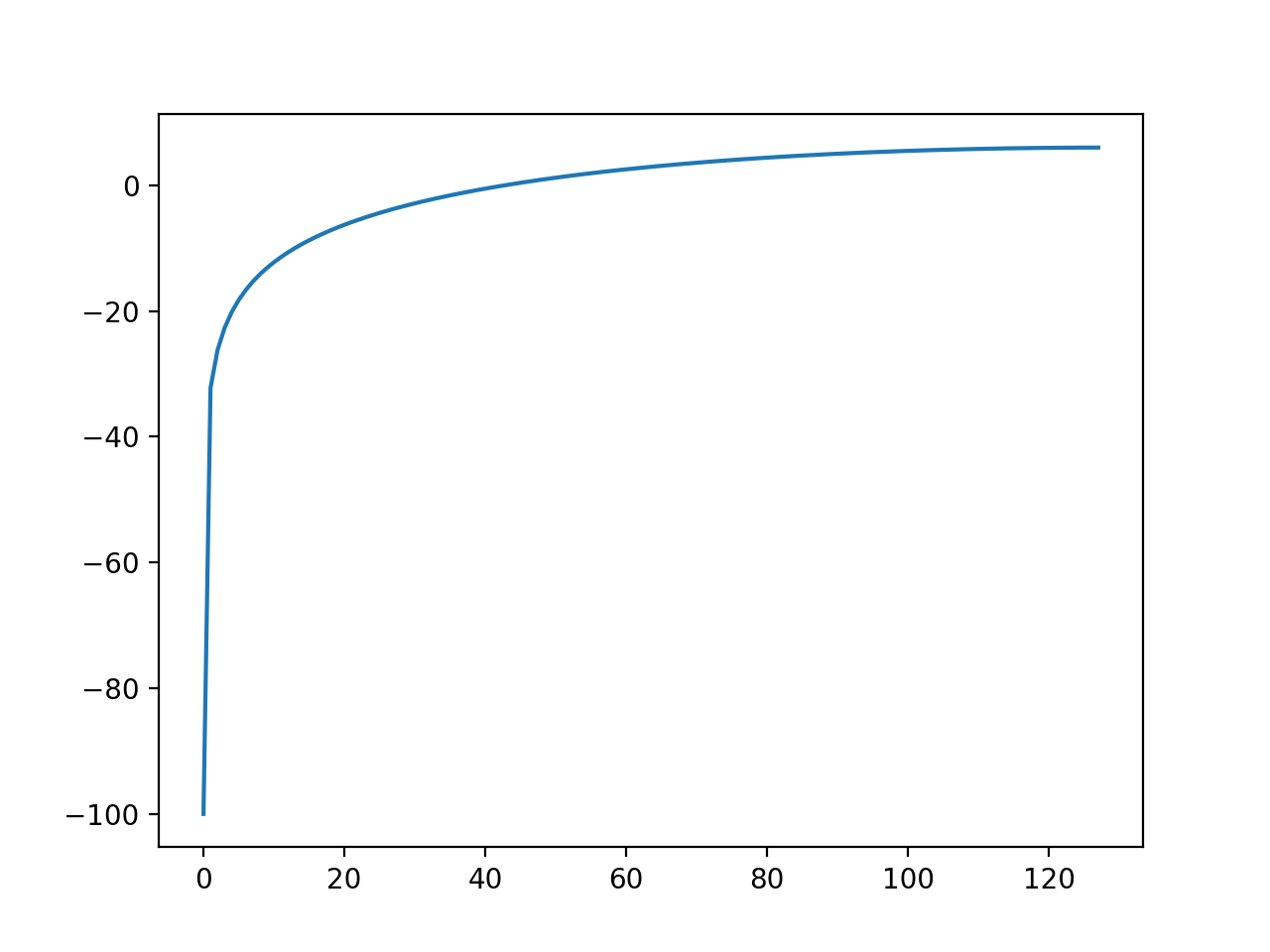
上記プログラムでは、[1,-1]の後ろに254点のゼロ値を連結し、全体で256点の信号列に仕立てています。その信号列に対してDFTを施して周波数領域に変換し、振幅スペクトラムをデシベルで算出しています。
どうやら、高域を通過し、低域を阻止するハイパスフィルタのような性質を持っているようです。
画像処理を学んだ事がある人であれば、例のカーネルはとなり同士の値の差分を求めるフィルタになっており、つまりハイパスフィルタ的に働くというのはすぐにわかると思います。
このようなフーリエ変換に基づく周波数的な考え方により、DFTで周波数応答を求めるという事でひとまずはある程度実用に耐えるのですが、各フィルタ係数が持つ意味がよくわからないため、自分が必要とする周波数特性を持つFIRフィルタ係数を作り出す事は難しいです。
数学的には、畳み込みの定理によって係数列と周波数領域が結びついているのですが、そんなことを言われてもよくわかりません。もう少し直感的に理解できる考え方が欲しいです。
そこで、今度は入力信号がインパルス信号だった場合とは逆に、カーネル側がインパルス信号だった場合を考えてみます。
カーネル側がインパルス信号ということは、[1]というカーネルになるということです。[1,0,0,0,0]とかでも構いませんが、ゼロ値の部分は内積計算の結果に影響を与えないため、[1]というカーネルと実質的に同じです。この[1]というカーネルによる畳み込み積分は、実質的に1を入力信号にかけていくのと同じなので、入力信号がそのまま出てきます。
import numpy
signal = [1,2,3,4,5,6]
kernel = [1]
numpy.convolve(signal, kernel)
# array([1, 2, 3, 4, 5, 6])
では、少しだけカーネルを変更して、インパルス信号には変わらないものの、タイミングをずらしてみるとどうなるでしょうか?つまり、[1]に余計なゼロ値を連結して、[0,1]にしてみます。
import numpy
signal = [1,2,3,4,5,6]
kernel = [0,1]
numpy.convolve(signal, kernel)
# array([0, 1, 2, 3, 4, 5, 6])
先ほどの結果と比べると、1点分だけ出力が後ろにずれていますね。では、カーネルの余分なゼロ値をもっと増やしてみましょう。
import numpy
signal = [1,2,3,4,5,6]
kernel = [0,0,0,0,0,0,0,0,1]
numpy.convolve(signal, kernel)
# array([0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6])
ゼロ値を連結した分だけ、入力信号がずれて出力されるようになりました。つまり、FIRフィルタのフィルタカーネル係数列の位置は、そのまま入力信号の出力タイミングになっているということがわかります。これを遅延と呼びます。
では、次に単純なインパルス信号ではなく、インパルスを二つ持つ信号でフィルタカーネルを作ってみるとどうなるでしょうか?
import numpy
signal = [1,2,3,4,5,6]
kernel = [1,0,0,0,0,0,0,0,1]
numpy.convolve(signal, kernel)
# array([1, 2, 3, 4, 5, 6, 0, 0, 1, 2, 3, 4, 5, 6])
強さ1のインパルスが存在する位置は入力信号をそのまま出力するので、入力信号が二回出力される結果になりました。
入力信号が短いため、出力側では信号が重なっていませんが、入力信号長とフィルタカーネル内のインパルスの間隔によっては、入力信号が重なり合った(加算された)状態で出力されるようになるはずです。
また、インパルスの値はそのまま入力信号に乗算されるため、0.5とすれば入力信号を半分に弱めてから出力することになります。
つまり、フィルタカーネルの係数が持つ単純な意味として、係数列の位置は遅延数、値は入力信号に対する倍率、そして、入力信号を遅延させつつ倍率をかけ、足し合わせた結果を出力する、という事がわかります。
ここまでは愚直に畳み込み積分の計算を追っていけば、大体理解できるところです。では、フィルタカーネルの系列と周波数特性にどのような関係があるでしょうか?
入力が周期信号の場合
今まで、入力は有限単発の信号でした。しかし、FIRフィルタカーネルの係数位置は遅延を意味することがわかったので、入力信号が仮に周期信号だった場合に、FIRフィルタカーネルもその周期間隔で係数が存在すると、入力信号を強めたり弱めたりできそうです。
試しに4点周期のインパルス列を入力信号とし、FIRフィルタカーネル側は一番目の要素が1、五番目の要素が-1、それ以外はゼロ値という係数列にしてみます。
import numpy
signal = [1,0,0,0,1,0,0,0,1,0,0,0]
kernel = [1,0,0,0,-1]
numpy.convolve(signal, kernel)
# array([ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0])
丁度5点目の入力時に、1点目の入力信号値にFIRフィルタカーネル五番目の-1が乗算された結果が加算されるため、signal[4] \times kernel[0] + signal[0] \times kernel[4] = 0となり、打ち消し合っています。要は、4点周期信号の入力に対して、5点目から入力信号を逆転させて足し合わせているわけです。
入力信号を2点周期にしてみても、一つとびで4点周期とみなせるため、やはり打ち消し合います。
import numpy
signal = [1,0,1,0,1,0,1,0,1,0,1,0]
kernel = [1,0,0,0,-1]
numpy.convolve(signal, kernel)
# array([ 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, -1, 0])
つまり、周期性と遅延は密接な関係があり、FIRフィルタカーネルの係数列として、どの位置で入力信号を強めるか、弱めるかというのは、入力信号のある周期の成分に対して強めたり弱めたりする効果がありそうだということです。
ここまでの実験は、手計算でも簡単に結果を導出できるように、整数列やインパルス列のみを使ってきました。しかし、これだけだと周波数特性との結びつきがまだ直感的にはわかりません。
そこで、サイン波を用いた実験をしてみます。
入力がサイン波の場合
サイン波は周期信号というだけでなく、特有の性質を持っています。同じ周波数のサイン波同士の足し合わせは、周波数は変わらず、位相と振幅を変化させるという性質です。
例えば、\piだけ位相がずれた同一振幅のサイン波同士を足し合わせた場合、結果のサイン波の振幅値はゼロ、つまり打ち消して無くなってしまいます。
このような、同一周波数のサイン波の足し合わせによる位相の変化、振幅の変化が、FIRフィルタによっても引き起こされているはずです。
試しに64点で周波数4のサイン波を作って、FIRフィルタを施してみます。周期は16点なので、8点で半周期です。FIRフィルタカーネルは1点目と9点目が1、それ以外はゼロです。
import numpy
import matplotlib.pyplot as plt
sine_wave = numpy.sin(numpy.linspace(0, 2 * numpy.pi * 4 * 63 / 64, 64))
result = numpy.convolve(sine_wave, [1,0,0,0,0,0,0,0,1])
plt.plot(sine_wave)
plt.plot(result)
plt.show()
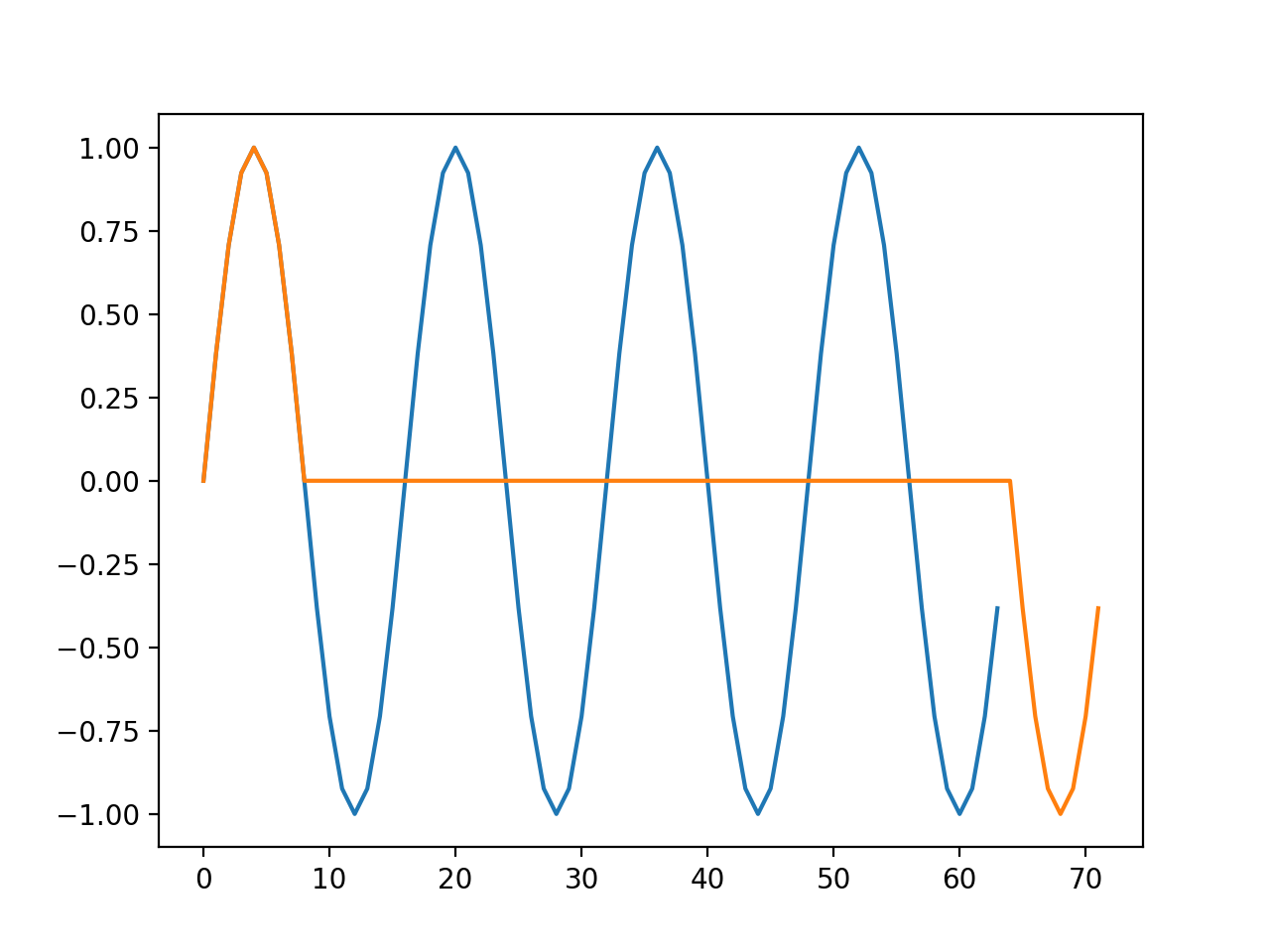
結果は下図の通りです。青が入力サイン波、オレンジが出力信号です。
FIRフィルタにより、丁度半周期ずれの入力信号を足し合わせ行くため、入力したサイン波形は見事に打ち消されています。
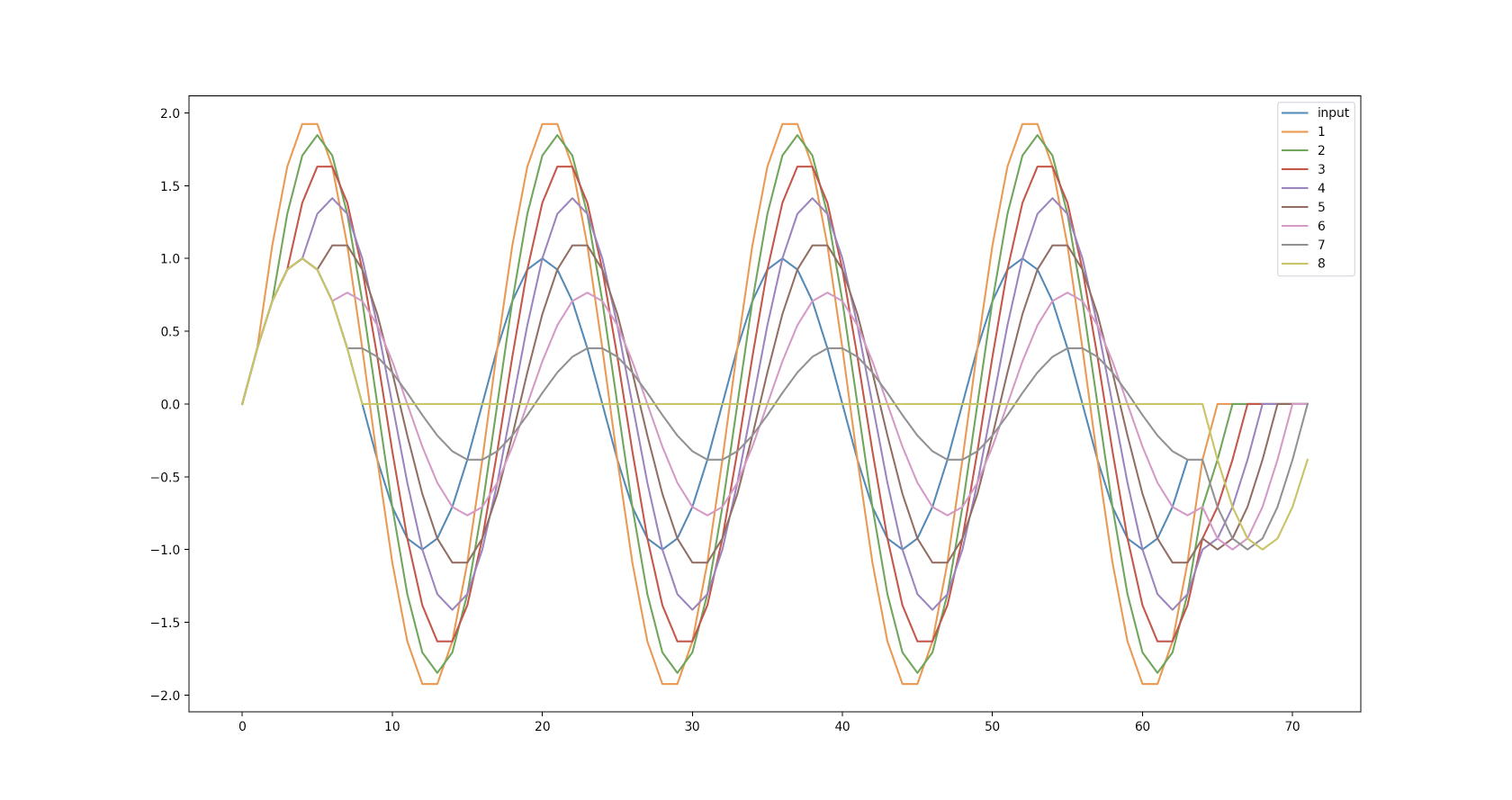
折角なので、1点ずれから8点ずれまでのFIRフィルタの結果を調べてみます。
import numpy
import matplotlib.pyplot as plt
sine_wave = numpy.sin(numpy.linspace(0, 2 * numpy.pi * 4 * 63 / 64, 64))
result1 = numpy.convolve(sine_wave, [1,1,0,0,0,0,0,0,0])
result2 = numpy.convolve(sine_wave, [1,0,1,0,0,0,0,0,0])
result3 = numpy.convolve(sine_wave, [1,0,0,1,0,0,0,0,0])
result4 = numpy.convolve(sine_wave, [1,0,0,0,1,0,0,0,0])
result5 = numpy.convolve(sine_wave, [1,0,0,0,0,1,0,0,0])
result6 = numpy.convolve(sine_wave, [1,0,0,0,0,0,1,0,0])
result7 = numpy.convolve(sine_wave, [1,0,0,0,0,0,0,1,0])
result8 = numpy.convolve(sine_wave, [1,0,0,0,0,0,0,0,1])
plt.plot(sine_wave, label="input")
plt.plot(result1, label="1")
plt.plot(result2, label="2")
plt.plot(result3, label="3")
plt.plot(result4, label="4")
plt.plot(result5, label="5")
plt.plot(result6, label="6")
plt.plot(result7, label="7")
plt.plot(result8, label="8")
plt.legend()
plt.show()
結果は下図の通りです。
FIRフィルタ側の遅延タイミングを遅らせていくと、入力サイン波の半周期に近づくほど振幅が小さくなり、半周期でゼロになります。また、遅延タイミングに応じて出力波形に現れるサイン波も遅延しています。
これらの事から、FIRフィルタは、入力サイン波に対して遅延と振幅倍率を施している事がわかります。
まとめ
信号をある区間で区切ってDFTにより周波数変換する場合、任意の入力信号は、様々な周波数のサイン波の足し合わせとして解釈できるのでした。FIRフィルタはつまり、任意の入力信号をサイン波の足し合わせと解釈した場合に、入力信号に含まれているあらゆる周波数のサイン波に対して、倍率をかけて遅延させる、という動作をしていると言えます。
この時の入力信号の増減、位相の変化は、FIRフィルタカーネルの係数列の強さやその位置によって決まってくるという事が今回の実験でわかりました。
また、最後の実験の結果からすると、あるFIRフィルタの係数が、特定の周波数のサイン波を綺麗に打ち消す周期で定義していたとして、それは他の周波数のサイン波からみると半端な周期の足し合わせになるため、増幅も減衰も半端な感じになりそうだということも推測できます。
この事は、FIRフィルタで帯域阻止する際の減衰特性が急峻ではなく、必ず目的周波数の周辺周波数もある程度巻き込んでしまう事の理由にもなっていそうです。