前回のあらすじと本記事の概要

FIRフィルタを行列表現すると巡回行列になりました。その巡回行列をさらに分解すると巡回置換行列で表現できる事がわかりました。本記事ではさらに巡回置換行列の性質を考えてみます。

前置き：特殊な行列たち

巡回行列(Circulant Matrix)

巡回行列とは、あるN次元のベクトル\vec{b} = [b_0, b_1, \cdots, b_{N-1}]を巡回させながら構成した行列です。

C=
\begin{pmatrix}
b_0&b_1&\cdots&b_{N-2}&b_{N-1} \\
b_{N-1}&b_0&\cdots&b_{N-3}&b_{N-2} \\
\vdots&\vdots& \ddots&\vdots& \vdots \\
b_2&b_3&\cdots&b_0&b_1 \\
b_1&b_2&\cdots&b_{N-1}&b_0 \\
\end{pmatrix}

具体例として4次元ベクトル\vec{b} = [b_0, b_1,b_2,b_3]の場合だと次の通りです。

C =
\begin{pmatrix}
b_0&b_1&b_2&b_3 \\
b_3&b_0&b_1&b_2 \\
b_2&b_3&b_0&b_1 \\
b_1&b_2&b_3&b_0 \\
\end{pmatrix}

置換行列(Permutation Matrix)

置換行列とは、各行各列に一つだけ1の要素を持ち、それ以外全部ゼロの正方行列です。
具体例として4次元のとある置換行列は以下の通りです。（同じ4次元でもどこに1を当てはめるかで様々なパターンが存在します。）

P=
\begin{pmatrix}
0&1&0&0 \\
1&0&0&0 \\
0&0&0&1 \\
0&0&1&0 \\
\end{pmatrix}

置換行列は、掛けられたベクトルの要素を単純に入れ替えるだけの行列です。試しに上記の具体例で示した置換行列を、4次元ベクトル\vec{x} = [x_0, x_1,x_2,x_3]にかけてみます。

P\vec{x}=
\begin{pmatrix}
0&1&0&0 \\
1&0&0&0 \\
0&0&0&1 \\
0&0&1&0
\end{pmatrix}
\begin{pmatrix}
x_0\\
x_1\\
x_2\\
x_3
\end{pmatrix}=\begin{pmatrix}
x_1\\
x_0\\
x_3\\
x_2
\end{pmatrix}

単位行列Iも掛けられたベクトルの各要素が元に戻ってくるとみなせるので、置換行列の特殊な場合です。

巡回置換行列とは

巡回行列かつ置換行列のことを私が勝手に巡回置換行列と呼んでいます。

つまり、要素のうちどれか一つだけ1、それ以外は全部ゼロのN次元の単位ベクトル\vec{e}=[0, 1, 0, \cdots, 0, 0]を巡回させながら構成した置換行列です。

P=
\begin{pmatrix}
0&1&0&\cdots&0&0\\
0&0&1&\cdots&0&0\\
\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\
0&0&0&\cdots&1&0\\
0&0&0&\cdots&0&1\\
1&0&0&\cdots&0&0\\
\end{pmatrix}

FIRフィルタによる畳み込み積分を行列で表現すると巡回行列になり、その巡回行列をさらに分解するとこの巡回置換行列で構成されていることがわかりました。今回の話はここから始まります。

巡回置換行列の冪乗の特性

N \times Nの巡回置換行列Pを単位行列IにN回かけると、また元の単位行列Iに戻ってくる事がわかります。

4次元の巡回置換行列で試してみます。

P=\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
\end{pmatrix}

PI=P^{1}I
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
\end{pmatrix}
\begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&1&0\\
0&0&0&1
\end{pmatrix}
=\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0
\end{pmatrix}

PPI=P^{2}I=
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0
\end{pmatrix}
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0
\end{pmatrix}
=\begin{pmatrix}
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
0&1&0&0
\end{pmatrix}

PPPI=P^{3}I=
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0
\end{pmatrix}
\begin{pmatrix}
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
0&1&0&0
\end{pmatrix}
=\begin{pmatrix}
0&0&0&1\\
1&0&0&0\\
0&1&0&0\\
0&0&1&0
\end{pmatrix}

PPPPI=P^{4}I=
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0
\end{pmatrix}
\begin{pmatrix}
0&0&0&1\\
1&0&0&0\\
0&1&0&0\\
0&0&1&0
\end{pmatrix}
=\begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&1&0\\
0&0&0&1
\end{pmatrix}
=I

4次元の巡回置換行列Pを4回かけることで、無事元に戻ってきました。どこから始めても巡回して戻ってくるので、N次元の巡回置換行列について以下の法則が成り立ちます。

\begin{aligned}
P^{0}&=&P^{N+0}&=&P^{2N+0}&=&\cdots&=&I\\
P^{1}&=&P^{N+1}&=&P^{2N+1}&=&\cdots&\\
P^{2}&=&P^{N+2}&=&P^{2N+2}&=&\cdots&\\
\vdots &\\
P^{-2}&=&P^{N-2}&=&P^{2N-2}&=&\cdots&\\
P^{-1}&=&P^{N-1}&=&P^{2N-1}&=&\cdots&\\
P^{0}&=&P^{N+0}&=&P^{2N+0}&=&\cdots&=&I\\
\end{aligned}

巡回しているのでいつかは元に戻るのは自明といえば自明です。この時、元に戻ってくるのはきっかり\pm N乗のタイミングです。これは次元数Nを法とした巡回群のように見えます。

巡回群自体の話は私もよくわからないので一旦脇に置いておきましょう。これ以降の説明では特に出てきません。

重要なのは、同じ巡回置換行列Pを掛け続けているのにまた元に戻ってくるという点です。行列ではなくスカラーにも同じような性質の数がありますね。そう、1です。1は何回かけても1のままです。もう一つすぐに思いつくのは-1です。-1は2回掛けると1に戻ってきます。

• 1回で元に戻る数は1
• 2回で元に戻る数は-1

3回や4回で元に戻る数は無いのでしょうか？

正則

巡回置換行列は正方行列です。正方行列の重要な性質の判断基準に「正則かどうか」があります。

n \times n正方行列Aが正則である、とは、以下の条件をみたす事を言います。（全部同値な条件なので、一つみたすならば他の条件を全て満たします。）

• 行列Aに対してAB=BA=Iとなる行列Bが存在する。（つまり逆行列が存在する）
• 行列式が非ゼロ（det A \neq 0）
• 行列のランクがrank A=n

さて、巡回置換行列は-1乗に相当する巡回置換行列が必ず存在するので、逆行列は存在していそうです。一般化した証明はできませんが、実際計算してみれば常に逆行列が存在します。

巡回置換行列の固有値と固有ベクトル

逆行列が存在するのであれば、巡回置換行列は固有値分解できます。正方行列は拡大縮小の成分の行列と、空間を回転するだけの成分の行列、元の空間へ戻す回転成分の行列の、3つの行列に分解する事ができます。これを固有値分解と呼びます。

実際に適当に選んだ巡回置換行列Pを固有値分解してみましょう。

P=
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
\end{pmatrix}

まずは固有値と固有ベクトルを求めます。行列Pの固有値は、以下の式をみたす非ゼロのスカラー値\lambdaと非ゼロベクトル\vec{u}です。

P \vec {u} = \lambda \vec{u}

つまり行列Pをかけても向きが変化せず、大きさだけスカラー値\lambda倍になるような非ゼロベクトル\vec{u}が存在する、という事です。
この等式の両辺から\lambda \vec{u}を減ずると以下の通りの式になります。

P \vec {u} – \lambda \vec{u} = \vec{0}

ここで、行列とベクトルの積に統一するために、\lambdaを\lambda Iという単位行列Iをかけた表現に置き換えます。\lambda I \vec{u} = \lambda \vec{u}です。計算してみれば一致することがわかります。

P \vec {u} – \lambda I \vec{u} = \vec{0}

これで行列とベクトルの積同士の減算になったので、行列積の線形性に従って行列積をくくり出します。

(P – \lambda I )\vec{u} = \vec{0}

巡回置換行列の固有値

行列とベクトルの積の結果がゼロになるということは、これは行列とベクトルの積で表現される連立方程式が解を持たないということです。つまり行列を構成するベクトルは一次従属の関係にあり、行列式はゼロになります。

det(P – \lambda I ) = 0

ここから、行列Pに上で適当に選んだ巡回置換行列Pの成分を当てはめてみて、行列式の対象となる行列を成分表現に展開します。

P – \lambda I=
\begin{pmatrix}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
1&0&0&0\\
\end{pmatrix} – \begin{pmatrix}
\lambda&0&0&0\\
0&\lambda&0&0\\
0&0&\lambda&0\\
0&0&0&\lambda\\
\end{pmatrix} = \begin{pmatrix}
-\lambda&1&0&0\\
0&-\lambda&1&0\\
0&0&-\lambda&1\\
1&0&0&-\lambda\\
\end{pmatrix}

さて、この行列の行列式がゼロになる\lambdaを求めれば良いことになります。

det \begin{pmatrix}
-\lambda&1&0&0\\
0&-\lambda&1&0\\
0&0&-\lambda&1\\
1&0&0&-\lambda\\
\end{pmatrix} = 0

2次や3次の行列式は公式があるので簡単に計算できますが、4次以上の行列式については一般化された公式が存在しません。かと言って次元数も多く、計算も難しいので、ここではSympyを使って行列式を計算してみます。

import sympy
P = sympy.Matrix([[0,1,0,0],[0,0,1,0],[0,0,0,1],[1,0,0,0]])
l = sympy.Symbol('λ')
equation = (P - l * sympy.eye(4)).det()
print(equation)
roots = sympy.solve(equation, l)
print(roots)

結果は以下の通りです。

λ**4 - 1
[-1, 1, -I, I]

つまり、方程式\lambda^4 – 1 = 0の\lambdaについての解（根：root）は(-1, 1, -i, i)の4つということです。4次方程式なので解が4つ得られ、重根はありません。

方程式の両辺に1を加えると、\lambda^4=1になるので、この解はつまり、4乗して1になる数だということがわかります。

巡回置換行列の固有値は1のN乗根

4乗して1になる数と言われれば、すぐに1だという事がわかります。また、少し考えれば-1も該当するという事がわかります。

虚数単位iが解に含まれている事が非自明な感じがします。2次方程式が常に解を持つためには、解を複素数まで拡張する必要がありました。複素数まで拡張することで、n次方程式は重根(重解)を含めてn個の根(解)を必ず持つのでした。

つまり、4乗して1になる数というのは複素数も含めれば必ず4つ存在するということです。

今まで例示してきた巡回置換行列は4次元だったので解も4つですが、これが5次元の巡回置換行列であれば\lambda^5=1、6次元であれば\lambda^6=1、N次元であれば\lambda^N=1という方程式の根を求める事になります。

さて、N乗しても1になる数というのは、実のところ2乗しても3乗しても大きさが1のままでなければなりません。大きさが1未満だった場合、掛けている内にどんどん小さくなっていきますし、1超過の場合は掛けている内にどんどん大きくなっていってしまいます。N乗して1に戻ってくるわけですから、その2乗である2N乗であっても1になるはずですし、2を変数Mに置き直してMをどんどん大きくしていっても\lambda^N=1なのですから、(\lambda^N)^M=\lambda^{NM}=1^M=1に決まっています。

つまり、巡回置換行列の固有値は全て大きさ1の数になる事がわかります。全て大きさが1だということは、複素数解も含めるという話だったので、巡回置換行列の全ての固有値はガウス平面上の単位円上に並ぶということです。

それでは単位円上にどのように固有値は並んでいるのでしょうか？再びN=4の場合に立ち返ってその固有値である(-1, 1, -i, i)をガウス平面上に書き込んでみましょう。

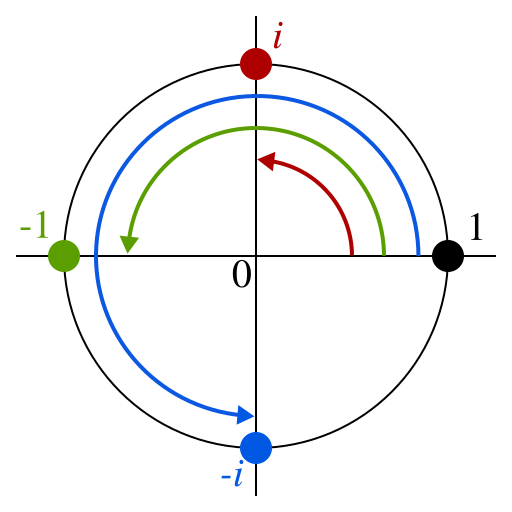
図１．1の4乗根をガウス平面上に配置

4つの解がちょうど単位円を4分割するように並びました。

iは1回掛ける度に反時計回りに90\degreeずつ回転していき、4回かけると1になります。-1は1回掛ける度に反時計回りに180\degreeずつ回転していき、2回掛けると1になります。-iは1回掛ける度に反時計回りに270\degreeずつ回転していき、2回掛けると540\degree=180\degreeなので-1、3回掛けると820\degree=90\degreeなのでi、4回掛けると1080\degree=0\degreeなので1になります。

全ての解は4乗した時点で必ず1に戻ってきます。つまり、4次元の巡回置換行列の固有値は1の4乗根になっているという事です。一般化すると、N次元の巡回置換行列の固有値は1のN乗根になります。

1のN乗根は、ガウス平面乗の単位円の円周上をN点で等分割した値です。定性的な性質は非常に単純です。固有値は正方行列をかけた時のスケール成分なので、元々N乗することで作用させるベクトルを元のベクトルに戻す巡回置換行列は、その固有値もN乗すれば1に戻り、大きさも常に1になるというのは自明と言えば自明ですね。

また、それぞれの1のN乗根は、1をのぞいて一番偏角の小さい値を\omegaとおくと、偏角の小さい順から1=\omega^0、\omega^1,\omega^2,\cdots,\omega^{N-1}となる事がわかります。

ちょうど\omegaずつ反時計回りに進んでいき、単位円上をほぼ一周するイメージです。

巡回置換行列の固有ベクトル

固有値が分かったので、以下の式にそれぞれの固有値を代入して方程式を解けば固有ベクトルを求めることができます。

(P – \lambda I )\vec{u} = \vec{0}

固有ベクトル\vec{u}の成分を(u_0, u_1, u_2, u_3)とします。

\begin{aligned}
(P – 1 I )\vec{u} = \begin{pmatrix}
-\lambda&1&0&0\\
0&-\lambda&1&0\\
0&0&-\lambda&1\\
1&0&0&-\lambda\\
\end{pmatrix} \begin{pmatrix}
u_0\\
u_1\\
u_2\\
u_3
\end{pmatrix} &=& \begin{pmatrix}
0\\
0\\
0\\
0
\end{pmatrix} \\
\begin{pmatrix}
-\lambda u_0 + u_1\\
-\lambda u_1 + u_2\\
-\lambda u_2 + u_3\\
-\lambda u_3 + u_0\\
\end{pmatrix} = \begin{pmatrix}
0\\
0\\
0\\
0\\
\end{pmatrix}
\end{aligned}

つまり、固有ベクトルの成分は以下の連立方程式を満たします。

\begin{aligned}
\lambda u_0 &=& u_1\\
\lambda u_1 &=& u_2\\
\lambda u_2 &=& u_3\\
\lambda u_3 &=& u_0\\
\end{aligned}

これを素直に計算すると、\lambda u_0 = u_1により\lambda \lambda u_0 = u_2、これをまた代入して\lambda \lambda \lambda u_0 = u_3、\lambda \lambda \lambda \lambda u_0 = u_0です。

\begin{aligned}
\lambda^1 u_0 &=& u_1\\
\lambda^2 u_0 &=& u_2\\
\lambda^3 u_0 &=& u_3\\
\lambda^4 u_0 &=& u_0\\
\end{aligned}

u_0を1とおくと、固有ベクトルの成分は固有値の冪乗になることがわかります。

\begin{aligned}
\lambda^1 &=& u_1 &\\
\lambda^2 &=& u_2 &\\
\lambda^3 &=& u_3 &\\
\lambda^4 &=& u_0&= 1\\
\end{aligned}

\vec{u} = (\lambda^0, \lambda^1, \lambda^2, \lambda^3)

あとは固有値を\omega^0,\omega^1,\omega^2,\omega^3としてそれぞれに対応する固有ベクトル\vec{u_0},\vec{u_1},\vec{u_2},\vec{u_3}を求めます。

\begin{aligned}
\vec{u_0} &= (\omega^{0\times0},\omega^{0\times1},\omega^{0\times2},\omega^{0\times3}) =& (1&,&1&,&1&,&1)\\
\vec{u_1} &= (\omega^{1\times0},\omega^{1\times1},\omega^{1\times2},\omega^{1\times3}) =& (1&,&\omega^1&,&\omega^2&,&\omega^3)\\
\vec{u_2} &= (\omega^{2\times0},\omega^{2\times1},\omega^{2\times2},\omega^{2\times3}) =& (1&,&\omega^2&,&\omega^4&,&\omega^6)\\
\vec{u_3} &= (\omega^{3\times0},\omega^{3\times1},\omega^{3\times2},\omega^{3\times3}) =& (1&,&\omega^3&,&\omega^6&,&\omega^9)\\
\end{aligned}

巡回置換行列の固有行列と対角化

固有ベクトルを並べた行列をここでは固有行列と呼びます。つまり、4次元の巡回置換行列Pの固有ベクトルを基にした固有行列Vは以下の通りです。

V=\begin{pmatrix}
\vec{u_0}\\
\vec{u_1}\\
\vec{u_2}\\
\vec{u_3}\\
\end{pmatrix} = \begin{pmatrix}
1&1&1&1\\
1&\omega^1&\omega^2&\omega^3\\
1&\omega^2&\omega^4&\omega^6\\
1&\omega^3&\omega^6&\omega^9
\end{pmatrix}

この固有行列Vが行列Pの回転を表す行列になります。そして、固有値を対角成分に並べた対角行列\Lambdaが、Pの拡大縮小成分になります。

\Lambda = \begin{pmatrix}
1&0&0&0\\
0&\omega^1&0&0\\
0&0&\omega^2&0\\
0&0&0&\omega^3
\end{pmatrix}

巡回置換行列の固有値は全て1のN乗根なので大きさが1です。そのため、\Lambdaの拡大縮小係数は全て大きさが1という事になります。これは何度かけても元のベクトルの大きさを変えないという事で、巡回置換行列の性質そのものを表していると言えます。

さて、Vと\Lambdaを使って行列Pを表します。

P = V \Lambda V^{-1}

つまり行列Pをあるベクトルに掛けた時の変換を分解すると、行列V^{-1}で空間を回転し、行列\Lambdaでスケーリングし、　行列Vでまた元の空間に戻す、という変換になります。

このように、行列をその固有値に基づいた空間の変換行列とスケーリングの行列に分解する事を固有値分解と呼びます。

この固有値分解の式を変形してみます。両辺に左からV^{-1}を掛け、右からVを掛けます。

\begin{aligned}
V^{-1}P &= V^{-1}V \Lambda V^{-1}V \\
V^{-1}PV &= I\Lambda I\\
V^{-1}PV &= \Lambda\\
\end{aligned}

行列Pの固有行列Vを使うと、行列Pを対角行列\Lambdaにする事ができました。この操作を行列の対角化と呼びます。

巡回置換行列の固有行列は離散フーリエ変換の変換行列

やっと本記事で最も主張したい部分に来ました。巡回置換行列Pの固有行列Vを改めて眺めてみましょう。

V = \begin{pmatrix}
1&1&1&1\\
1&\omega^1&\omega^2&\omega^3\\
1&\omega^2&\omega^4&\omega^6\\
1&\omega^3&\omega^6&\omega^9
\end{pmatrix}

これはどこかでみたことがある行列ですね。\omegaは1のN乗根なので、N=4の場合は4を法として\omega^nは巡回します。つまり、以下の通りに書き直すことができます。

V = \begin{pmatrix}
1&1&1&1\\
1&\omega^1&\omega^2&\omega^3\\
1&\omega^2&1&\omega^2\\
1&\omega^3&\omega^2&\omega^1
\end{pmatrix}

ここでは\omega=iなので、上記の行列成分に代入すると……。

V = \begin{pmatrix}
1&1&1&1\\
1&i&-1&-i\\
1&-1&1&-1\\
1&-i&-1&i
\end{pmatrix}

これを行ベクトル単位でプロットしてみましょう。

import matplotlib.pyplot as plt
import numpy
w0 = numpy.array([1j ** (i * 0) for i in range(4)])
w1 = numpy.array([1j ** (i * 1) for i in range(4)])
w2 = numpy.array([1j ** (i * 2) for i in range(4)])
w3 = numpy.array([1j ** (i * 3) for i in range(4)])
w0fig = plt.subplot(4,1,1)
w1fig = plt.subplot(4,1,2)
w2fig = plt.subplot(4,1,3)
w3fig = plt.subplot(4,1,4)
w0fig.plot(range(4), w0.real)
w0fig.plot(range(4), w0.imag)
w1fig.plot(range(4), w1.real)
w1fig.plot(range(4), w1.imag)
w2fig.plot(range(4), w2.real)
w2fig.plot(range(4), w2.imag)
w3fig.plot(range(4), w3.real)
w3fig.plot(range(4), w3.imag)
plt.tight_layout()
plt.show()

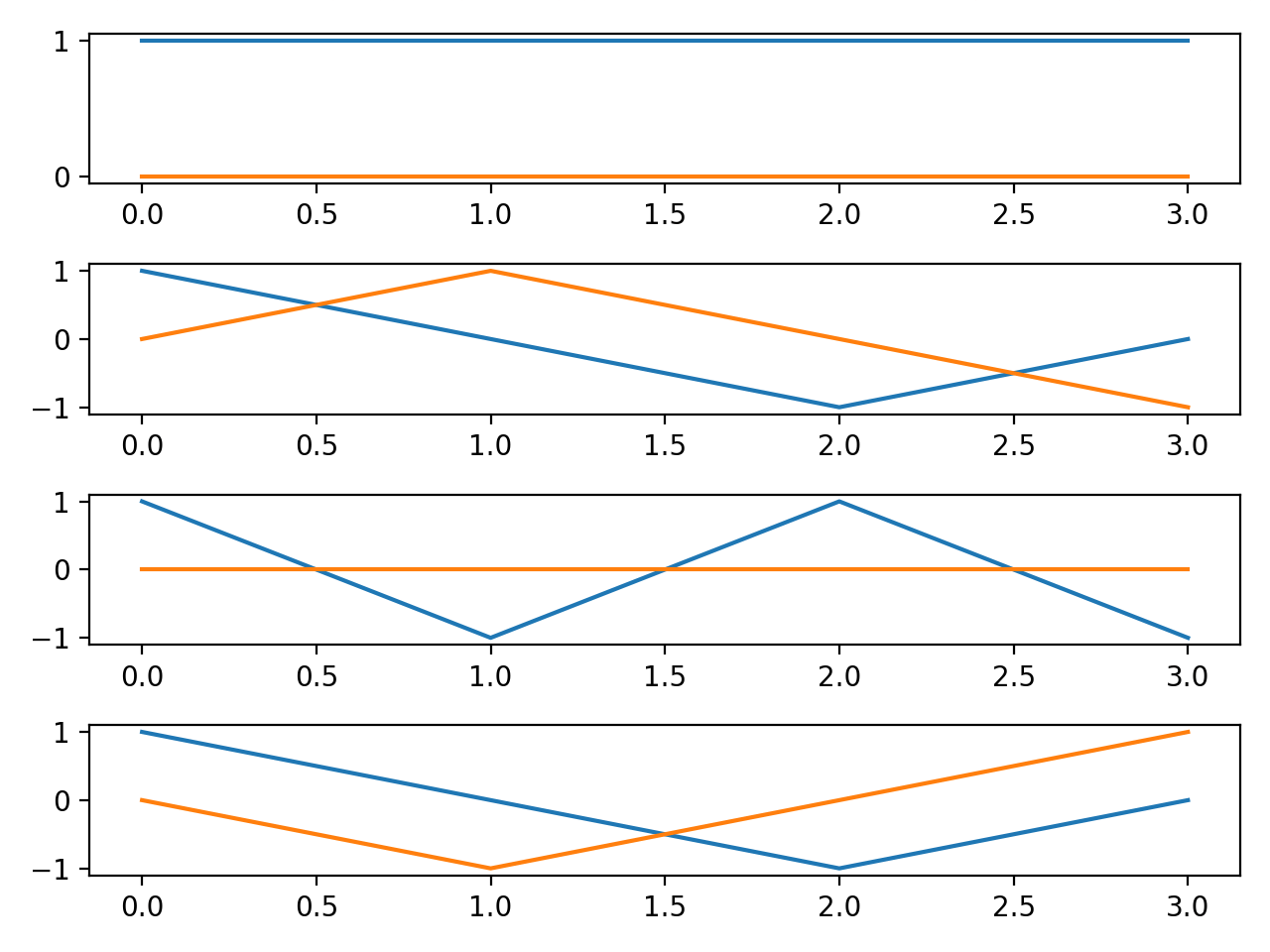図２．N=4の固有ベクトル群

なんだかわかりづらいですね。なので次元数を16にあげてやり直してみます。

import matplotlib.pyplot as plt
import sympy
import numpy
n = 4 # プロットで敷き詰めやすいので実験では平方数に限定する
N =  n ** 2 # 次元数は平方数
l = sympy.Symbol('λ')
w_array = sympy.solve(l**N - 1) # 1のN乗根を全て求める
args = [sympy.arg(v) for v in w_array] # 1のN乗根から偏角を求める
sorted_pairs = sorted(zip(args, w_array)) # 偏角と根をペアにして偏角でソート
w = sorted_pairs[(N + 1)//2][1] # 0の次の偏角に対応する根を取り出す
for k in range(N):
    basis = numpy.array([complex(w ** (i * k)) for i in range(N)]) # 固有ベクトルを生成して数値化
    subfig = plt.subplot(n, n,k+1)
    subfig.plot(range(N), basis.real)
    subfig.plot(range(N), basis.imag)

plt.tight_layout()
plt.show()

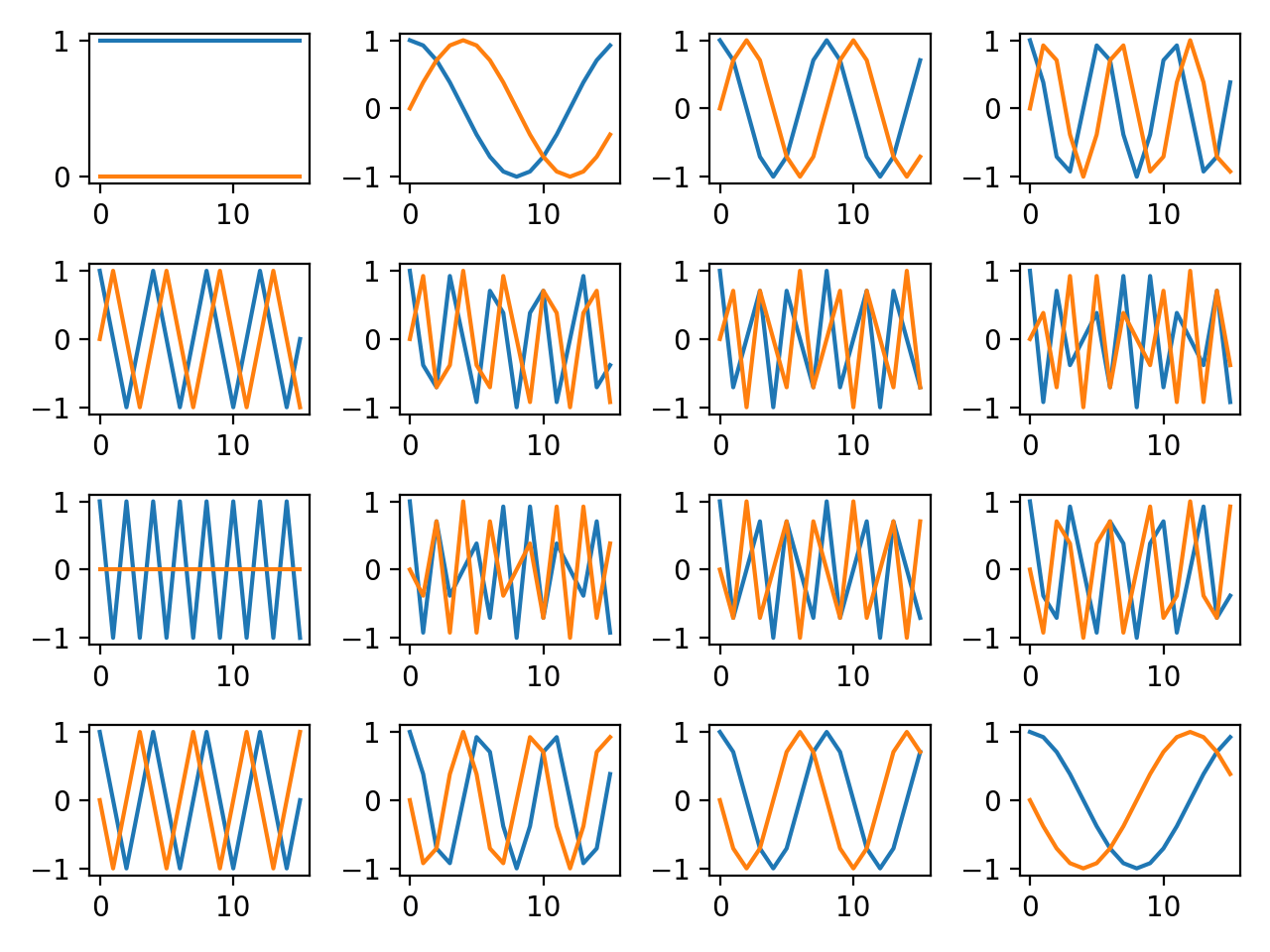
図３．N=16の固有ベクトル群

あっ！これ進研ゼミでやったところだ！

そうです。これは離散フーリエ変換の変換行列です。嘘だと思うなら前述のPythonコードのnをもっと大きな値に設定してプロットしてみてください。

驚くべきことに、巡回置換行列の固有行列を求めると離散フーリエ変換の変換行列が得られるのです。そして、これはつまり巡回置換行列を離散フーリエ変換と逆変換で対角化できるということです。

巡回置換行列の出所は畳み込み和の行列表現でした。つまり、畳み込み和を離散フーリエ変換で対角化できるという事です。

次の記事では畳み込み和の対角化と畳み込みの定理の導出を試みます。