はじめに

ものの本にはあまりはっきりと書かれていなかったりしますが、線形代数を学習すると、離散フーリエ変換(DFT)は三角関数によって構成された直交基底を用いた直交変換だということがわかります。

ここでは、三角関数で直交基底を構成することの意味を確認します。

三角関数の直交性

まず、根本的な話として、DFTはsin関数の整数倍周波数とcos関数の整数倍周波数の有限個の組み合わせで正規直交基底を構成します。

DFTだけが直交基底を構成する唯一の方法というわけではなく、例えばcos関数のみで直交基底を構成するDCTや、矩形波の分割統治的な適用で構成するDHT(離散アダマール変換)、他にも自作のベクトルからシュミットの直交化法を用いて正規直交基底を構成する方法等が存在します。

どのような正規直交基底を用いるかで、その結果得られる周波数成分の持つ情報の意味が異なります。

とりわけ音声信号の解析ではDFTが用いられ、画像処理や情報圧縮の分野ではDCTやDHTが用いられる事が多いようです。

三角関数の直交性の話に戻ります。

ある周波数のsin波形を１周期分取り出し、位相を少しずつずらした波形と内積をとると、どのようになるでしょうか？

import numpy
import sys
import matplotlib.pyplot as plt


def make_sin(N, f):
    angles = numpy.linspace(0, (f * N - f) / N, N) * 2 * numpy.pi
    return numpy.sin(angles)

if __name__ == "__main__":
    N = 64
    f = 1

    sin_vec = make_sin(N, f)

    result = []
    for phase in range(N):
        shifted_sin_vec = numpy.r_[sin_vec[N - phase:], sin_vec[:N - phase]]
        square_norm = numpy.sum(sin_vec**2)
        square_inner_poduct = (numpy.dot(sin_vec, shifted_sin_vec) / square_norm) ** 2
        result.append(square_inner_poduct)

    plt.plot(result, marker='.', label="square inner poduct")
    plt.plot(sin_vec, marker='.', label="sin vector")
    plt.legend()
    plt.show()

    sys.exit(0)

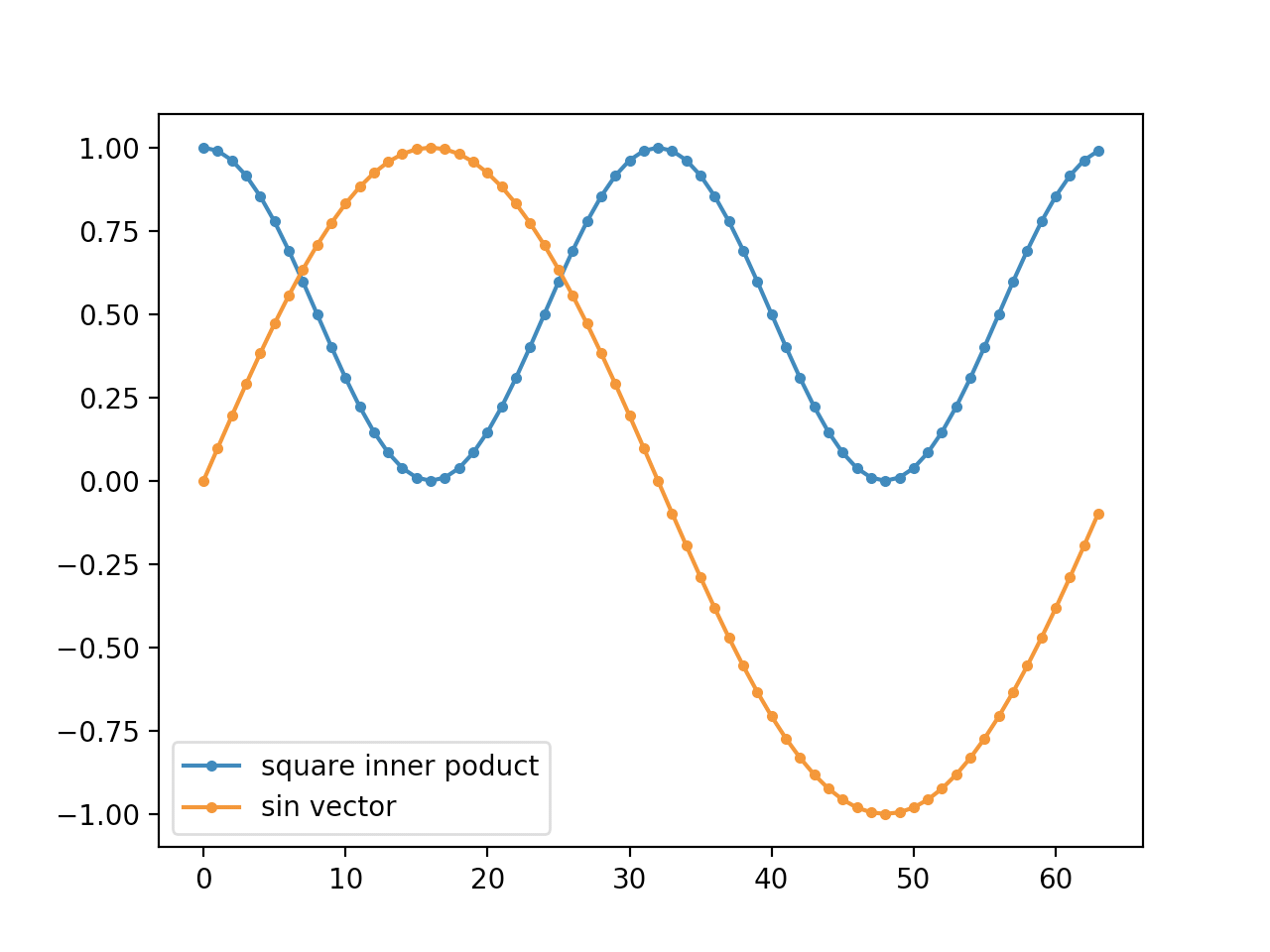
上記のコードは、周波数１の64次元sin波形ベクトルを生成し、位相をずらしながら内積を計算しています。

グラフで見やすいスケールに収めるために、内積は正規化し、ゼロが極小値となるように自乗しています。

結果は以下のとおりです。

結果を見ると、４分の１周期のところと４分の３周期のところで内積がゼロになっている、つまり直交していることがわかります。

sin関数の位相を４分の１周期ずらした関数といえば、cos関数です。この結果は、同じ周波数のsin関数とcos関数が直交している事を示しています。

sin関数とcos関数に対する内積を同時に求める

今度は少し凝った実験をしてみます。sin波形ベクトルの位相をずらしながら、位相固定のsin波形ベクトルとcos波形ベクトルの二つと同時に内積を求め、その関係を図示してみます。

import numpy
import sys
import matplotlib.pyplot as plt

def __make_sin(N, f):
    angles = numpy.linspace(0, (f * N - f) / N, N) * 2 * numpy.pi
    return numpy.sin(angles)

def __make_cos(N, f):
    angles = numpy.linspace(0, (f * N - f) / N, N) * 2 * numpy.pi
    return numpy.cos(angles)

def __rotate_array(array, offset):
    return numpy.r_[array[offset:], array[:offset]]

def __L2_normalize(vector):
    if numpy.linalg.norm(vector) == 0:
        return vector
    return vector / numpy.linalg.norm(vector)

if __name__ == "__main__":
    N = 64
    f = 1

    sin_vec = __L2_normalize(__make_sin(N, f))
    cos_vec = __L2_normalize(__make_cos(N, f))

    sin_component_array = []
    cos_component_array = []
    for phase in range(N):
        rotated_sin_vec = __rotate_array(sin_vec, phase)
        sin_component = numpy.dot(sin_vec, rotated_sin_vec)
        cos_component = numpy.dot(cos_vec, rotated_sin_vec)
        sin_component_array.append(sin_component)
        cos_component_array.append(cos_component)

    L2_norm_array = numpy.linalg.norm(numpy.c_[sin_component_array, cos_component_array], axis=1)
    argument_array = numpy.arctan2(cos_component_array, sin_component_array) / numpy.pi
    plt.plot(sin_component_array, marker='.', label="sin component")
    plt.plot(cos_component_array, marker='.', label="cos component")
    plt.plot(L2_norm_array, marker='.', label="L2 norm")
    plt.plot(argument_array, marker='.', label="argument")
    plt.legend()
    plt.show()

    sys.exit(0)

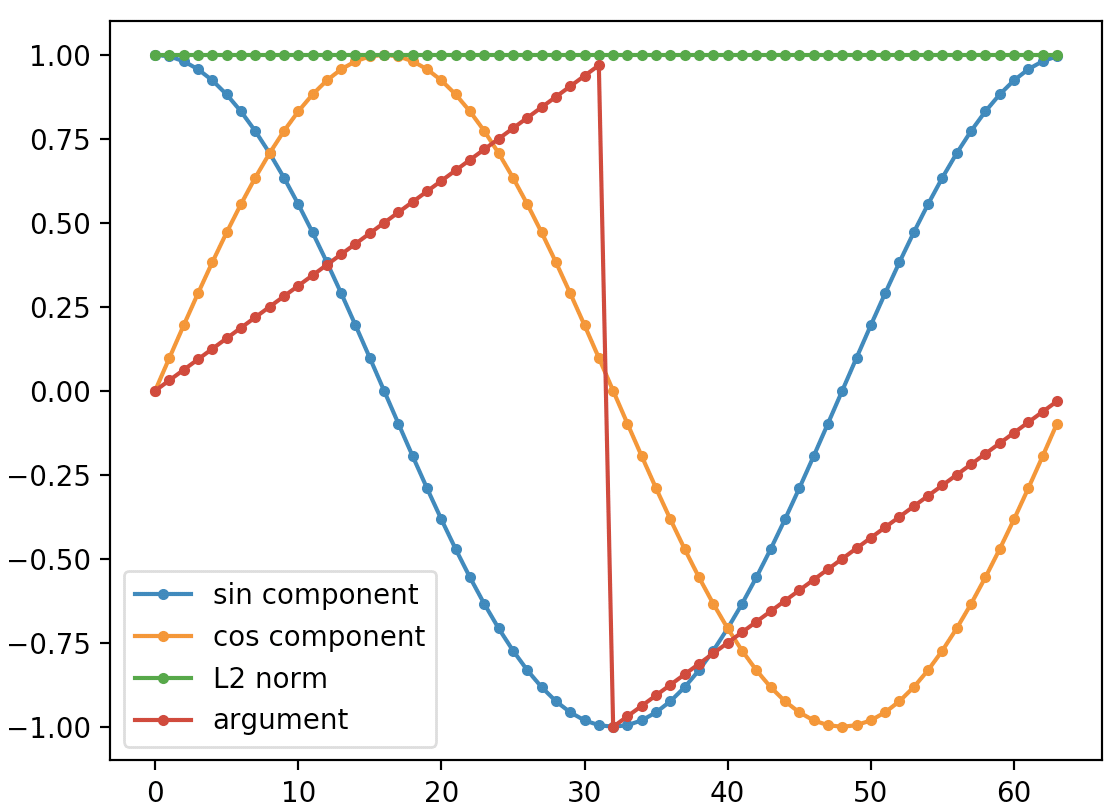
大きさ1のsin波形ベクトルとcos波形ベクトルを生成し、それぞれに対して、sin波形ベクトルの位相を1サンプルずつ進めながら内積を計算しています。

大きさ1のベクトル同士の内積を計算しているため、その計算結果は-1 \sim 1の範囲に必ず収まります。0は直交を、1は同じベクトルを、-1は反転したベクトルを意味します。

要は、同じ周波数のsin波形ベクトルとcos波形ベクトルをそれぞれ基底とみなし、位相を変化させたsin波形ベクトルをその二つの基底ベクトルの線型結合で表そう、という実験です。

位相0の瞬間では、sin波形ベクトルはsin基底に対して内積が1、cos基底に対して内積が0です。位相をずらしていくと徐々にsin基底成分は減っていき、逆にcos基底成分は増えていきます。周期の\frac{1}{4}まで位相をずらしたところで、sin基底成分とcos基底成分の関係は逆転し、sin基底成分は0、cos基底成分は1となりました。

sin波形ベクトルの位相を\frac{1}{4}周期進めるとcos波形ベクトルとなり、同周波数のsin波形ベクトルとは直交することは事前の実験で確かめた通りです。

つまり、sin波形ベクトルの位相を進めていくと、sin基底成分の増減と逆の位相で、cos基底成分が増減するということがわかります。

次に、このsin基底成分とcos基底成分の関係を見てみます。

まず、sin基底成分とcos基底成分をペアとして、一つのベクトルとみなしてみます。このとき、sin基底成分とcos基底成分からなるベクトルの大きさ（L2ノルム）は、sin波形ベクトルの位相によらず常に1です。

これはつまり、入力された特定周波数のsin波形ベクトルの大きさを、位相によらず抽出できる事を意味します。今回の実験では正規化周波数1のsin基底とcos基底を用いているので、入力ベクトルの中から正規化周波数1の成分を、位相に依存しない形で抜き出しているという事です。

次に、sin基底成分とcos基底成分からなるベクトルの偏角を考えます。二次元ベクトルなので、単純に極座標平面状に配置したと考えて偏角を計算してみると、位相0の瞬間を偏角0度として、sin波形ベクトルの位相が進むに従って、偏角も進んでいる事がわかります。

これはつまり、入力された特定周波数のsin波形ベクトルの位相を、その大きさによらず抽出できる事を意味します。

以上のことから、ある周波数のsin基底とcos基底は違いに直交し、それぞれを用いた線型結合によってある入力ベクトルから基底成分を抜き出す操作は、同周波数のsin波形がどの程度の大きさ、位相で入力ベクトルに含まれているのかを抽出する操作だと言えます。

位相に対する振幅スペクトラムの不変性

DFTはsin基底とcos基底を組み合わせた直交基底による線形変換です。よって、DFTは入力信号の位相に対して不変な振幅スペクトラムを得られるはずです。

実験して見ましょう。

整数正規化周波数における振幅スペクトラムの推移

import numpy
import sys
import mpl_toolkits.mplot3d
import matplotlib.pyplot as plt
import scipy.fftpack

def __make_sin(N, f):
    angles = numpy.linspace(0, (f * N - f) / N, N) * 2 * numpy.pi
    return numpy.sin(angles)

def __L2_normalize(vector):
    if numpy.linalg.norm(vector) == 0:
        return vector
    return vector / numpy.linalg.norm(vector)

def __plot_3d(data, title):
    Axes3D = mpl_toolkits.mplot3d.Axes3D
    ax = Axes3D(plt.figure())
    x_limit = data.shape[1]
    y_limit = data.shape[0]
    x, y = numpy.meshgrid(numpy.arange(0,x_limit,1), numpy.arange(0,y_limit,1))
    ax.plot_surface(x, y, data, cmap='Spectral')
    plt.title(title)
    plt.show()
    plt.close()

if __name__ == "__main__":
    N = 64
    f = 4

    sin_wave = __L2_normalize(__make_sin(N*2, f*2))
    fft = scipy.fftpack.fft
    wave_array = numpy.ndarray(shape=(N, N))
    amp_spectrogram = numpy.ndarray(shape=(N, N//2))
    for i in range(N):
        wave_array[i] = sin_wave[i:i+64]
        amp = numpy.abs(fft(sin_wave[i:i+64])[:N//2]) / numpy.sqrt(N)
        amp_db = 20 * numpy.log10(amp + sys.float_info.min)
        amp_spectrogram[i] = amp_db

    __plot_3d(wave_array, "Phase shifted Sin Waves")
    __plot_3d(amp_spectrogram, "Amplitude Spectrogram")

    sys.exit(0)

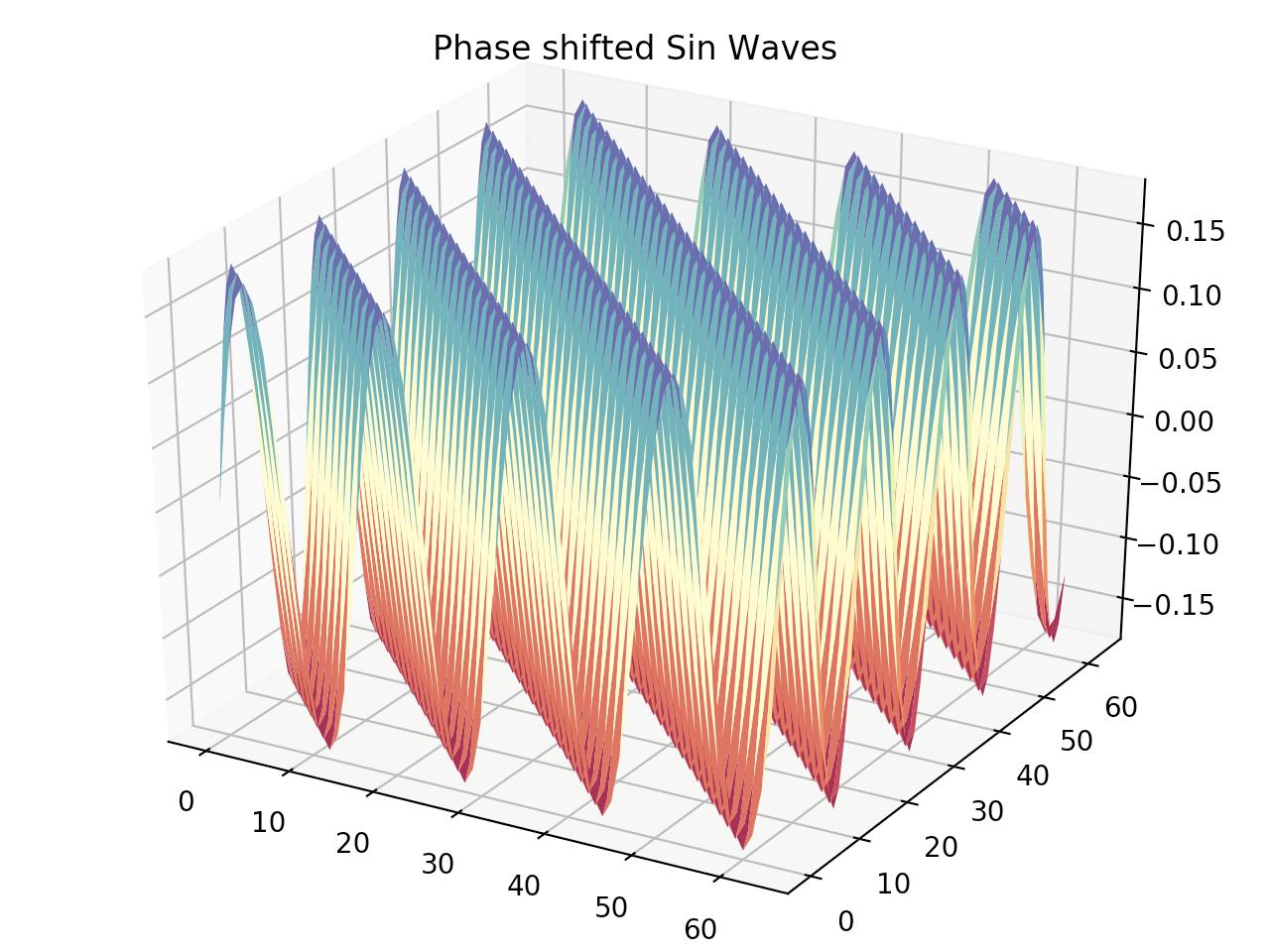
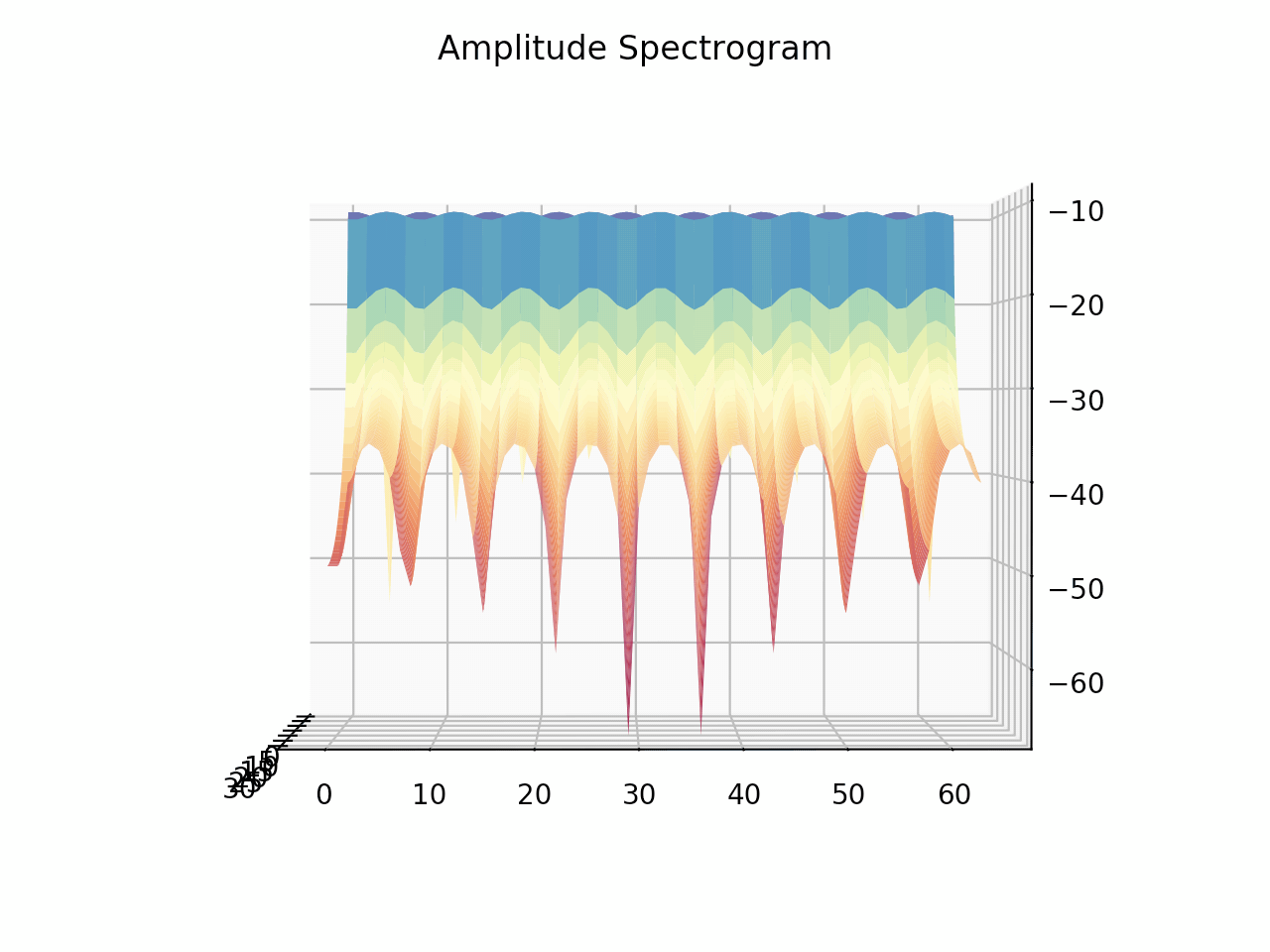
まずは周期長64サンプル、正規化周波数4のサイン波形を、2周期分生成します。
このサイン波形の参照位置を1サンプルずつずらしながらDFTを施していき、振幅スペクトラムを得ます。
振幅スペクトラムはデシベル化しています。

最後に、1サンプルずつずらしながら参照したサイン波形と、それを元にDFTで算出した振幅スペクトログラムを3次元メッシュ表示しています。

結果は以下の通りです。

わずかですが、本来の周波数成分以外の成分が出ており、位相から影響を受けている事がが図からわかります。

非整数正規化周波数における振幅スペクトラムの推移

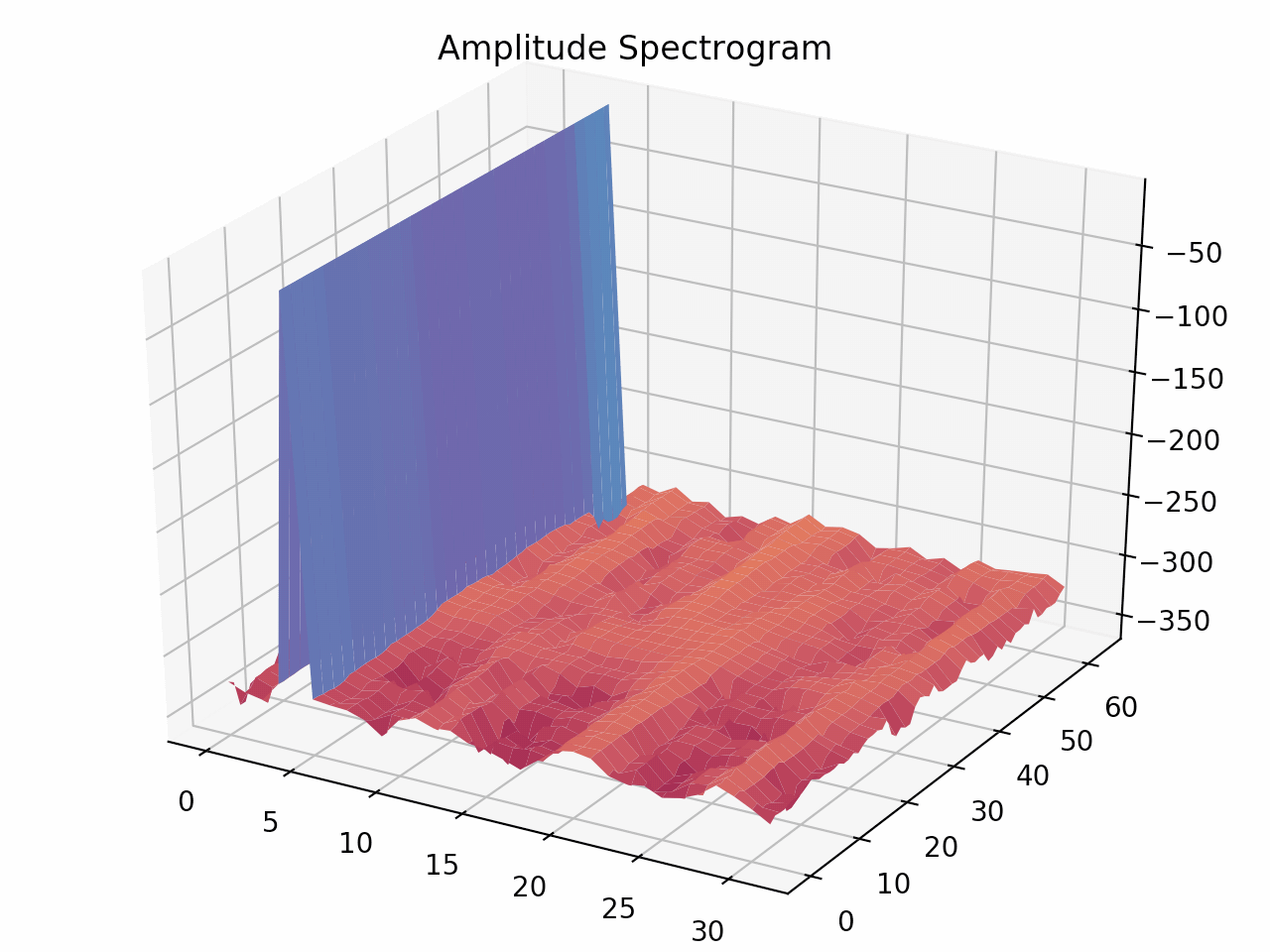
次に、正規化周波数を4.5という中途半端な周波数にして再実験して見ます。中途半端な正規化周波数にすることで、サイドローブの影響がわかりやすくなるはずです。

前述のプログラムの変数fを4.5とするだけです。

図からも分かる通り、非整数周波数の場合は位相による影響を非常に強く受けています。

非整数周波数の図を回転して見ます。

位相の変化に応じてサイドローブ成分が激しく揺れています。その落差、実に20デシベル以上です。また、ピーク周波数のビン位置も揺れており、正確な周波数もわかりにくくなっています。

理論的には振幅値は位相に影響を受けないのですが、コンピュータ上で生成したサイン波形は真に理想的なサイン波形でない限り、本来の周波数以外の成分が内積により0にならず、成分が出てきてしまいます。

このように単一周波数信号ですら、信号に対する分析窓の位相、および分析対象の信号の性質を見極めないと、直感的には受け入れがたい結果が得られるので注意が必要です。

また、安易に計算誤差とひとまとめにせず、何によってどのように影響を受けるのかを把握しておく事が重要だと考えます。

今回の実験では三角関数の位相と直交性から、DFTは位相に対して不変な振幅値を求める計算であることを演繹的に導き出しました。

しかし、実際の計算となるとDFT基底のsin関数やcos関数の精度、および分析対象のサイン波形の精度に依存して、位相の変化に対して振幅スペクトラムのサイドローブ成分が大きく変動する場合がある事を確認しました。

まとめ

途中で極座標の考え方は出てきたものの、今回の実験では複素数を用いていません。離散フーリエ変換（DFT）の線形代数からのアプローチとしては、今回の実験の考え方が参考になると考えます。

今回の実験で使用した、sin基底とcos基底を組み合わせた基底表現は、まさしく離散フーリエ変換の基底ベクトルそのものです。複素数やe^{-i \omega t}といった表現を理解しなくても、離散フーリエ変換が何をしているのか、線形代数的なアプローチから直感的に理解できるのではないでしょうか。

また、実際の計算の際には計算誤差をどうしても無視でず、単純な方法だけでは理想的な計算結果が得られない場合がある事もわかりました。

多くの周波数分析の場面では、位相成分は捨てられてしまいますが、位相の概念、計算の都合を正しく把握しておく事が重要だと考えます。