信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。
Read more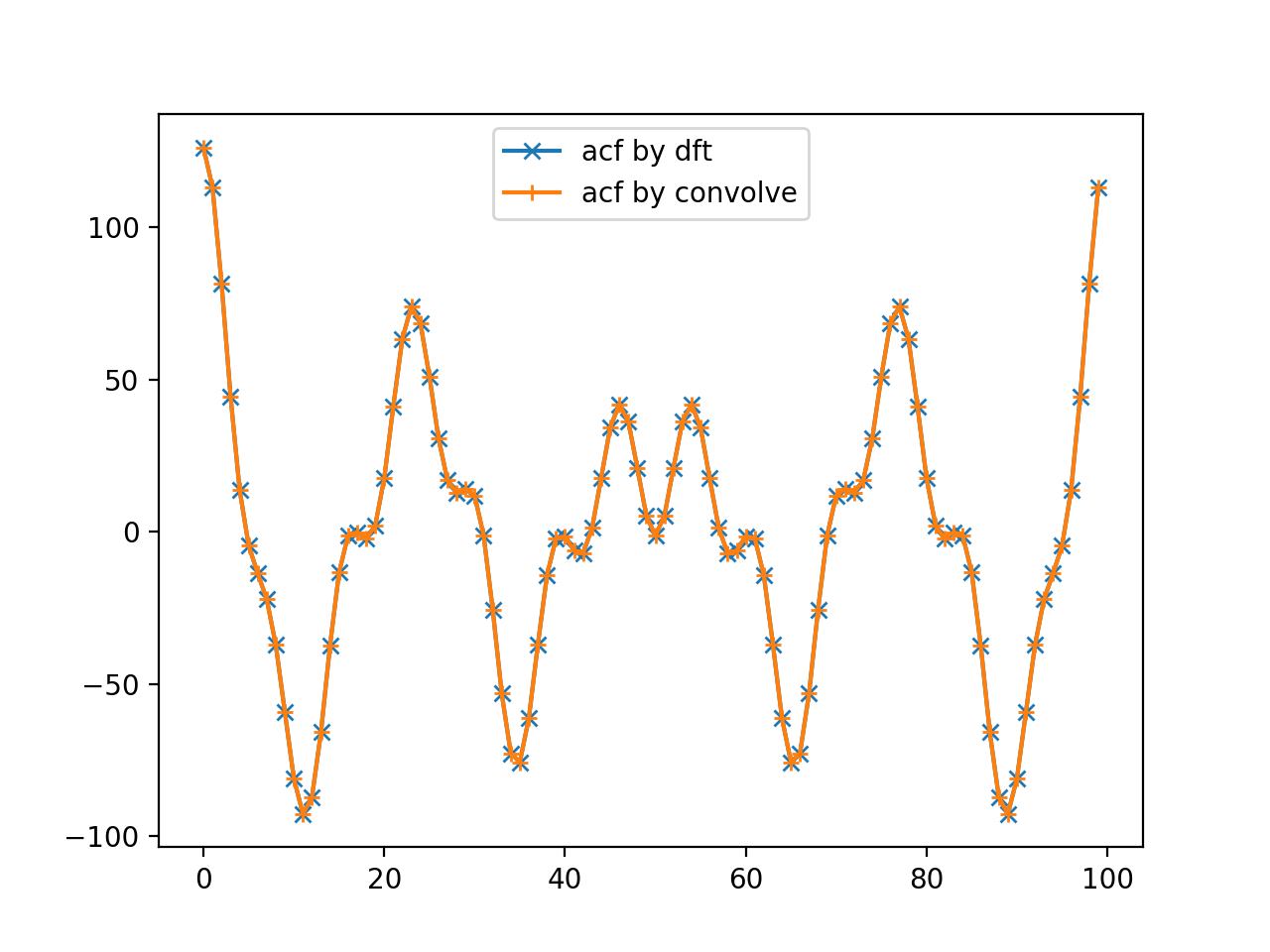
信号処理を勉強する

信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。
Read more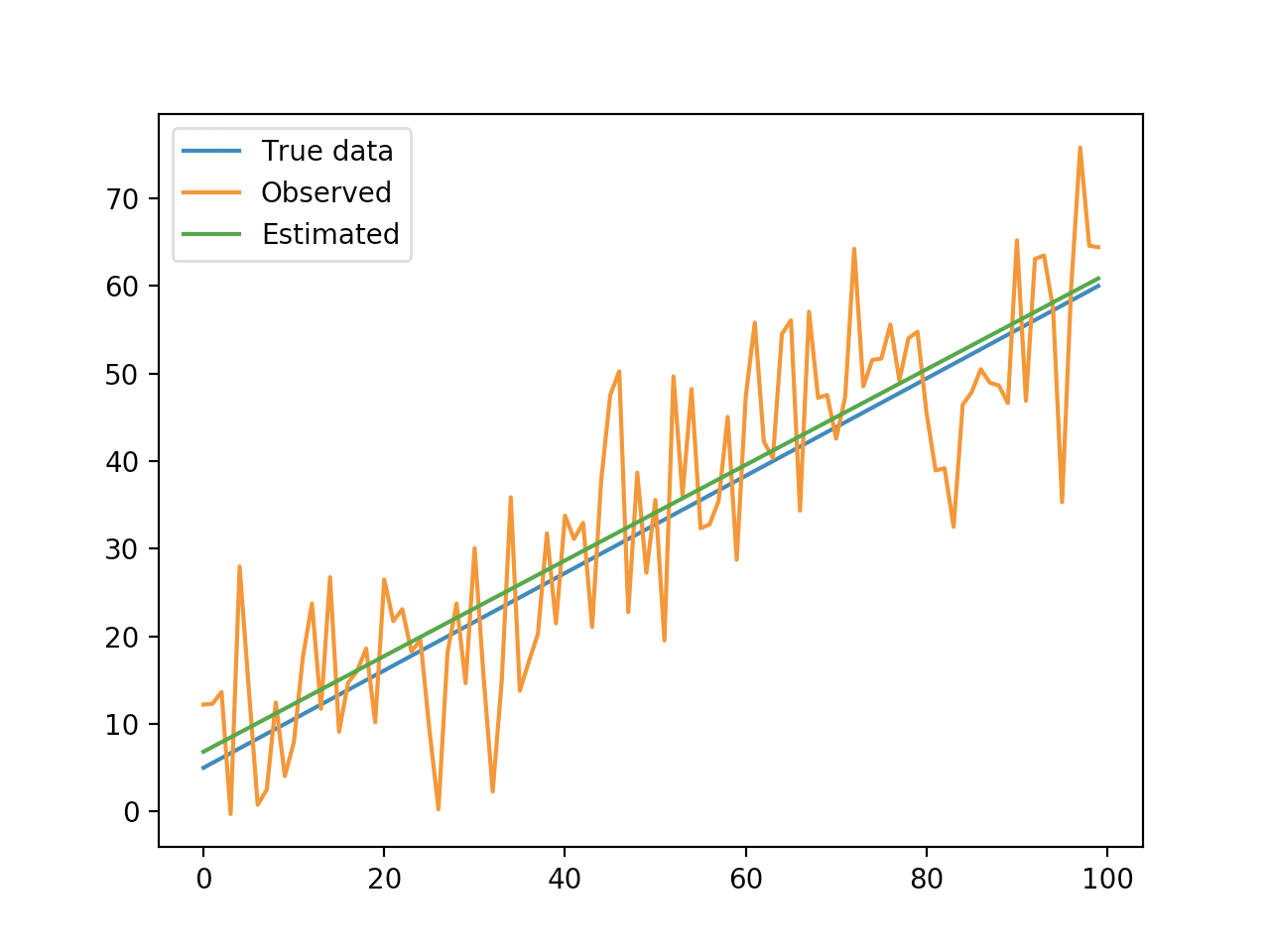
はじめに 信号処理は解析学だけではなく統計学を必要とすることもあります。信号処理を抽象化すれば、数列から何かしらの処理により特徴量を抽出する処理だと言えます。今回は趣向を変えて、線形回帰分析を取り扱って見ます。
Read more
はじめに ものの本にはあまりはっきりと書かれていなかったりしますが、線形代数を学習すると、離散フーリエ変換(DFT)は三角関数によって構成された直交基底を用いた直交変換だということがわかります。 ここでは、三角関数で直交
Read moreはじめに DFTの各基底ベクトルは複素ベクトルのため、DFTによって得られた結果も複素ベクトルです。つまり、結果の各要素は複素数であり、実部と虚部を持ちます。 結果の複素ベクトルの各要素に対して、複素数の大きさを計算した
Read moreデシベルは信号の強さ、大きさを人間の感覚尺度に合わせたスケールです。 人間の感覚は入力信号に対して指数関数的な鈍さを持っているので、入力信号を対数化すると、人間の感じ方に違いスケールになります。
Read more