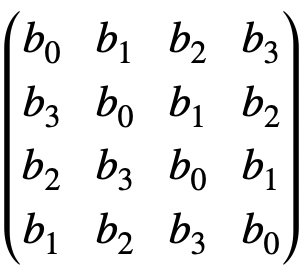はじめに

FIRフィルタは畳み込み積分とよく言われますが、そもそも畳み込み積分と言われてもそれがなんなのかよくわかりません。そこで、身近な線形代数の知識を使ってFIRフィルタを行列で表現し、その特性を調べてみます。

FIRフィルタと畳み込み積分

FIRフィルタは、入力信号に対して位置をずらしながら係数列であるFIRフィルタカーネルとの内積を計算することです。この「位置をずらしながらフィルタカーネルとの内積を計算していく」計算の事を畳み込み積分と呼びます。

例えば入力信号を8点、FIRフィルタカーネルを4点としてこの計算を行列で考えてみます。
入力信号のどの範囲までFIRフィルタの処理対象とするか次第ですが、ここでは入力信号の先頭からFIRフィルタを施し、都合の良い範囲までフィルタカーネルの後ろにゼロ値を挿入して考えます。

内積の計算は、ゼロ値の要素が結果に影響を与えないため、ゼロ値を挿入することで計算の都合の良い長さにベクトルの次元数を増やすことができます。

$[1,2,3,4] \cdot [1, 1, 1, 1] = [1,2,3,4,0,0,0,0] \cdot [1,1,1,1, 0,0,0,0]=10$
(ここでの $\cdot$ 記号はベクトル同士の内積演算記号です。)

8点の入力信号ベクトルを $\vec{P} = [p_0,p_1,p_2,p_3,p_4,p_5,p_6,p_7]$ 、4点FIRフィルタカーネルを $\vec{F} = [f_0,f_1,f_2,f_3,0,0,0,0]$ と、ゼロ値を連結して8点にしておきます。

FRIフィルタはフィルタカーネルと入力信号とで内積を計算する位置をシフトしていく計算のため、位置をずらした場合のFIRフィルタカーネルを、 $\vec{F}$ をずらして構成します。

$\begin{aligned} \vec{F_0} &= [f_0, f_1, f_2, f_3, 0, 0, 0, 0] \\ \vec{F_1} &= [0, f_0, f_1, f_2, f_3, 0, 0, 0] \\ \vec{F_2} &= [0, 0, f_0, f_1, f_2, f_3, 0, 0] \\ \vec{F_3} &= [0, 0, 0, f_0, f_1, f_2, f_3, 0] \\ \vec{F_4} &= [0, 0, 0, 0, f_0, f_1, f_2, f_3] \\ \vec{F_5} &= [f_3, 0, 0, 0, 0, f_0, f_1, f_2] \\ \vec{F_6} &= [f_2, f_3, 0, 0, 0, 0, f_0, f_1] \\ \vec{F_7} &= [f_1, f_2, f_3, 0, 0, 0, 0, f_0] \\ \end{aligned}$

後ろ３つの $\vec{F_5}$ 、 $\vec{F_6}$ 、 $\vec{F_7}$ は $\vec{F}$ の末尾を巡回させて構成します。ここの成分はもともと入力信号とフィルタカーネルの内積を計算するのに長さが足りていない成分なので、本来の計算結果は $\vec{F_0} \sim \vec{F_4}$ との内積までだと考えましょう。 $\vec{F_5}$ 、 $\vec{F_6}$ 、 $\vec{F_7}$ まで用意したのは、入力次元数と出力次元数を合わせるためです。入力次元数と出力次元数が一致するということは、 $N \times N$ の正方行列になるということです。

これを行列の計算に置き換えます。 $\vec{F}$ で作ったベクトルをまとめて行列 $F$ とすると、具体的な計算式は以下の通りです。

$F \vec{P} = \left( \begin{array}{cccccccc} f_0&f_1& f_2&f_3&0&0&0&0 \\ 0&f_0&f_1& f_2&f_3&0&0&0 \\ 0&0&f_0&f_1& f_2&f_3&0&0 \\ 0&0&0&f_0&f_1& f_2&f_3&0 \\ 0&0&0&0&f_0&f_1& f_2&f_3 \\ f_3 &0&0&0&0&f_0&f_1&f_2 \\ f_2&f_3&0&0&0&0&f_0&f_1 \\ f_1&f_2&f_3&0&0&0&0&f_0 \end{array} \right) \left( \begin{array}{c} p_0 \\ p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \\ p_6 \\ p_7 \\ \end{array} \right)$

この行列 $F$ ですが、１列目を巡回させて構成しているので巡回行列と呼びます。

つまり、FIRフィルタの畳み込み積分とは、フィルタカーネルベクトルを巡回させて巡回行列を構成し、入力ベクトルに巡回行列を掛ける事と同じです。

この巡回行列の線形代数上の特性を調べていく事で、畳み込み積分とは何かを線形代数を通して理解できるはずです。

巡回行列と置換行列

巡回行列の構成方法をもう少し分解して捉えてみます。次元数が多いと大変なので、ここでは4次元で考えてみます。
ベクトル $[b_0, b_1, b_2, b_3]$ を基本とした巡回行列 $B$ を考えます。

$B = \left( \begin{array}{cccc} b_0&b_1&b_2&b_3 \\ b_3&b_0&b_1&b_2 \\ b_2&b_3&b_0&b_1 \\ b_1&b_2&b_3&b_0 \\ \end{array} \right)$

この行列 $B$ を、基本としたベクトルの各要素を一つだけ持つように分解してみます。

$\begin{aligned} B_0 &= \left( \begin{array}{cccc} b_0&0&0&0 \\ 0&b_0&0&0 \\ 0&0&b_0&0 \\ 0&0&0&b_0 \\ \end{array} \right) \\ B_1 &= \left( \begin{array}{cccc} 0&b_1&0&0 \\ 0&0&b_1&0 \\ 0&0&0&b_1 \\ b_1&0&0&0 \\ \end{array} \right) \\ B_2 &= \left( \begin{array}{cccc} 0&0&b_2&0 \\ 0&0&0&b_2 \\ b_2&0&0&0 \\ 0&b_2&0&0 \\ \end{array} \right) \\ B_3 &= \left( \begin{array}{cccc} 0&0&0&b_3 \\ b_3&0&0&0 \\ 0&b_3&0&0 \\ 0&0&b_3&0 \\ \end{array} \right) \\ \end{aligned}$

このように分解することで、巡回行列 $B$ を以下の通りに行列 $B_0 \sim B_3$ の加算で表現できます。

$B = B_0 + B_1 + B_2 + B3$

さらに行列 $B_0 \sim B_3$ は、ゼロ以外の要素値はそれぞれ一種類しか無いので、「スカラー $\times$ 行列」の形に分解する事ができます。

$\begin{aligned} B_0 &= b_0 \left( \begin{array}{cccc} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ \end{array} \right) \\ B_1 &= b_1 \left( \begin{array}{cccc} 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ \end{array} \right) \\ B_2 &= b_2 \left( \begin{array}{cccc} 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ 0&1&0&0 \\ \end{array} \right) \\ B_3 &= b_3 \left( \begin{array}{cccc} 0&0&0&1 \\ 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ \end{array} \right) \\ \end{aligned}$

全ての行列について、行、列共に要素 $1$ を一つだけ持つ行列、置換行列で構成されていることがわかりました。置換行列は入力ベクトルを単に並び替えるだけの行列です。

置換行列は入力ベクトルの要素を並び替えて出力ベクトルを作り出すだけの行列です。と、いうことは、出力ベクトルに何度も置換行列を施していくと、最終的に入力ベクトルに戻ってくるのでしょうか？

ここで行列 $B_1$ を構成している置換行列に注目します。行列 $B_1$ を構成している置換行列をもう一度掛けると、行列 $B_2$ を構成している置換行列になることに気づいたでしょうか？

$\begin{aligned} \left( \begin{array}{cccc} 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ \end{array} \right) \times \left( \begin{array}{cccc} 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ \end{array} \right) &= \left( \begin{array}{cccc} 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \\ 0&1&0&0 \\ \end{array} \right) \end{aligned}$

実は行列 $B_3$ を構成している置換行列も、行列 $B_2$ 同様に行列 $B_1$ を構成している置換行列を３回掛けることで表現できます。（計算は省略します。）

ここで行列 $B_1$ を構成している置換行列に $C$ という名前をつけましょう。行列の掛け算も複数回の掛け算をべき乗で表現できるので、 $C$ を使って改めて行列 $B_0 \sim B_3$ を表現しなおします。

$\begin{aligned} B_0 &= b_0 C^0 \\ B_1 &= b_1 C^1 \\ B_2 &= b_2 C^2 \\ B_3 &= b_3 C^3 \end{aligned}$

そして、巡回行列 $B$ は行列 $C$ を使って次の通りに表現できます。

$B = b_0 C^0 + b_1 C^1 + b_2 C^2 + b_3 C^3 = \sum_{i=0}^{3}{b_{i} C^{i}}$

行列 $C$ は置換行列ですが、さらに巡回する作用も持っているので、私はこれを巡回置換行列と勝手に呼んでいます。

これを $N$ 次元のフィルタカーネル $[b_0, b_1, \cdots, b_{N-1}]$ に一般化すると、巡回行列 $B$ は以下のようにフィルタカーネルの各要素と巡回置換行列 $C$ の冪乗の総和になります。

$B = b_0 C^0 + b_1 C^1 + \cdots + b_{N-1} C^{N-1} = \sum_{i=0}^{N-1}{b_{i} C^{i}}$

「畳み込み積分」と一言で済まされていた背景を線形代数という視点で紐解くと、このような構造が裏にあるのです。

おわりに

今回は一旦ここまでで説明を区切ります。ひとまず畳み込み積分と言われているFIRフィルタの計算を行列で表現できるようになりました。

スライドさせながらフィルタカーネルと内積を計算する、という操作をシンプルな行列計算に落とし込む事ができたので、この行列計算の特性を調べていくことでさらに理解を深める事ができそうです。