はじめに

今回はピッチ推定ツールから派生して、自己相関関数を時系列に並べて分析するためのツールの作成と、出力した時系列自己相関関数のデータをSonic Visualiserで可視化してみます。

時系列でデータを作って可視化する事で、どこに問題があるか、改善の糸口はどこか、直感を働かせやすくなります。

時系列自己相関関数を出力するツールの実装

ピッチ推定ツールと内容はほぼ同じです。ピッチ推定処理を自己相関関数を算出する処理に置き換えたのと、一次元の時系列データしか出力できなかった関数を、二次元以上のデータを出力するように変更しています。

import argparse
import os.path
import numpy
import scipy.io.wavfile
import scipy.fftpack
import scipy.signal

def __lpcms_int16_to_float(lpcms):
    lpcm_array = []
    for index, lpcm in enumerate(lpcms):
        lpcm_array.append(numpy.divide(lpcm.astype(float), 32767.0))
        lpcms = numpy.array(lpcm_array)
    return lpcms

def __read_wave_file_to_float(wave_file_name):
    fs, data = scipy.io.wavfile.read(wave_file_name)
    nch = 1
    if type(data[0]) == numpy.ndarray:
        lpcms = data.transpose()
        nch = len(lpcms)
    else:
        lpcms = numpy.array([data])
    pcm_type_from_file = type(lpcms[0][0])
    if pcm_type_from_file == numpy.int16:
        lpcms = __lpcms_int16_to_float(lpcms)
    return fs, nch, lpcms

def __split_lpcm(lpcm, stride, width):
    n = int(numpy.floor((len(lpcm) - width) / stride))
    extended_length = n * stride + width
    if len(lpcm) < extended_length:
        lpcm = numpy.r_[lpcm, numpy.zeros(extended_length - len(lpcm))]
    splited_lpcms = []
    for index in range(0, n):
        offset = index * stride
        splited_lpcms.append(lpcm[offset:offset + width])
    return numpy.array(splited_lpcms)

def __acf_by_dft(values):
    power_spectrum = numpy.abs(scipy.fftpack.fft(values)) ** 2
    return numpy.real(scipy.fftpack.ifft(power_spectrum))

def __acf(fragment, window_function):
    windowed = numpy.multiply(fragment, window_function)
    padded = numpy.r_[windowed, numpy.zeros(len(windowed))]
    acf = __acf_by_dft(padded)[:len(windowed)]
    if acf[0] != 0:
        acf /= acf[0]
    return acf

def __output_series_csv_file(output_filepath, series_data, stride):
    def __float_to_str(v):
        return str(int(v * 1000000) / 1000000)
    rows = [",".join(map(__float_to_str, values)) for values in series_data]
    csv_rows = [f'{stride * i},{row}' for i, row in enumerate(rows)]
    with open(output_filepath, "wt") as csv_file:
        csv_file.write("\n".join(csv_rows))
    return None

def __main(input_wave_filepath, window_size, stride):
    fs, nch, lpcms = __read_wave_file_to_float(input_wave_filepath)
    window_half_size = args.window_size // 2
    fragments = __split_lpcm(lpcms[0], stride, window_size)

    window_function = scipy.signal.blackmanharris(window_size)
    acf_array = [__acf(fragment, window_function) for fragment in fragments]

    basename = os.path.basename(input_wave_filepath)
    __output_series_csv_file(basename + "_acf.csv", acf_array, stride)
    return None

if __name__ == "__main__":
    argment_parser = argparse.ArgumentParser()
    argment_parser.add_argument("-i", "--input_wave_filepath", type=str, required=True)
    argment_parser.add_argument("-w", "--window_size", type=int, default=512)
    argment_parser.add_argument("-s", "--stride", type=int, default=128)
    args = argment_parser.parse_args()

    __main(args.input_wave_filepath, args.window_size, args.stride)

    exit(0)

処理の概要

ほぼピッチ推定ツールと同じです。
今回はピッチ推定を行わなず、自己相関関数を時系列で出力するだけです。

def __acf(fragment, window_function):
    windowed = numpy.multiply(fragment, window_function)
    padded = numpy.r_[windowed, numpy.zeros(len(windowed))]
    acf = __acf_by_dft(padded)[:len(windowed)]
    if acf[0] != 0:
        acf /= acf[0]
    return acf

自己相関関数のゼロ番目の要素は自分自身の信号との相関値（自乗総和）になり、これが自己相関関数内での最大値でもあります。

そこで、自己相関関数のゼロ番目の要素値で自己相関関数全体を割れば、自己相関関数全体を-1 \sim 1の範囲に正規化できます。

この時、入力データは全部ゼロだった場合だけ自己相関関数のゼロ番目の要素値が0になってしまうため、ゼロ除算を避ける条件判定を入れています。

def __output_series_csv_file(output_filepath, series_data, stride):
    def __float_to_str(v):
        return str(int(v * 1000000) / 1000000)
    rows = [",".join(map(__float_to_str, values)) for values in series_data]
    csv_rows = [f'{stride * i},{row}' for i, row in enumerate(rows)]
    with open(output_filepath, "wt") as csv_file:
        csv_file.write("\n".join(csv_rows))
    return None

CVS出力処理は本質的な部分では無いですが、今回は出力データサイズがそこそこ大きくなるため、あまり大きくなりすぎないように工夫しています。

float値をそのまま文字列化してCSV出力してしまうと場合によっては非常に長い文字列になってしまい、データサイズも大きくなってしまいます。

可視化用の出力なのでそこまで精度はいらないので、精度を落としてから文字列化する処理__float_to_str関数を自作して、自己相関関数値にmapで適用しています。

ちなみに、ここで小サイズ化の工夫をしなかった場合、窓長にもよりますが私の手元では200MiBを超えました。実験データで毎回200MiB超えは扱いにくいですし、読み込みにも時間がかかったりするので、分析精度に悪影響がないのであればデータは小さい方が良いです。

    window_function = scipy.signal.blackmanharris(window_size)
    acf_array = [__acf(fragment, window_function) for fragment in fragments]

実際に　LPCM断片から自己相関関数を計算するところは、人出力がそれぞれ１要素ずつになったのでリスト内包表記１行で実装しています。

実行

実験用データ

今回も実験用データとしてピッチ推定ツールで使ったJSUT-Songを使います。

質の良い日本語独唱音声は用意が難しいので、JSUT-Songの存在は非常にありがたいです。

実行方法

さて、以下の通りに実行すると、003.wav_acf.csvというファイルを出力します。

$ python time_series_acf.py -i ./data/jsut-song_ver1/child_song/wav/003.wav

Sonic Visualiserによる可視化

出力した時系列自己相関関数をSonic Visualiserで可視化してみましょう。

まずは元となったWAVEファイルをSonic Visualiserで開きます。

図1. 単純にWAVEファイルを開く

次に、メニューの「Pane」から「Add New Pane」で新しいペインを追加します。

図2. ペインの追加

ペインを追加したら、新しく追加したペインに003.wav_acf.csvを読み込みます。メニューの「Open」から003.wav_acf.csvを読み込みましょう。１列目は時間オフセット値と解釈させる必要があります。「Time」になっていればOKです。ピッチ推定ツールと同じくサンプル数単位の値にしてあるので、「Explicitly, in audio sample frames」を選びましょう。

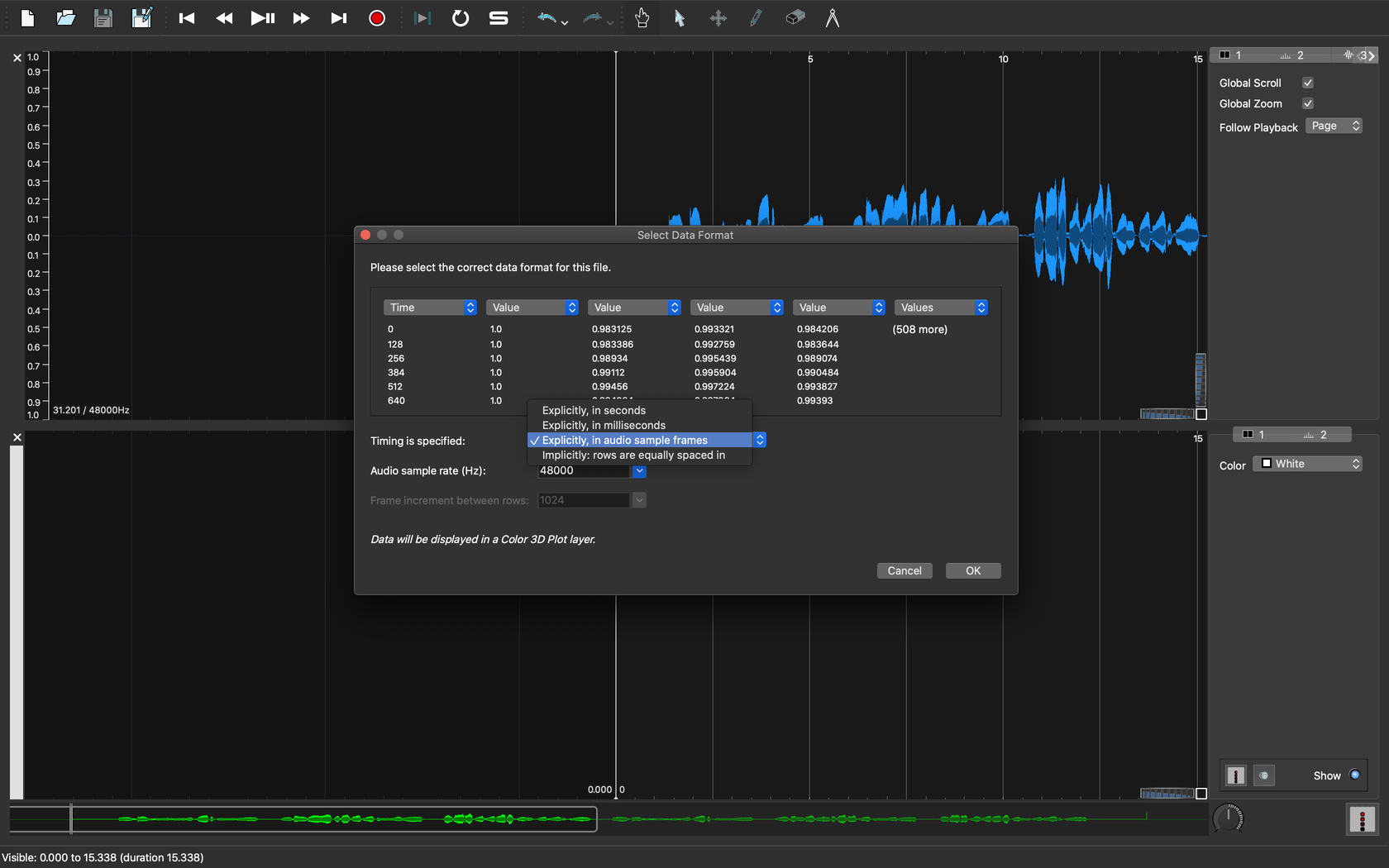図3. ペインに時系列自己相関関数データを読み込む

読み込んだ結果が図4になります。Sonic Visualiserは二次元以上の時系列データを読み込むと、自動的に画像化してくれます。Visualiserの名前は伊達ではありません。なお、デフォルトでは緑から赤のカラーマップで表示されますが右側の設定パネルでカラーマップを変更できます。

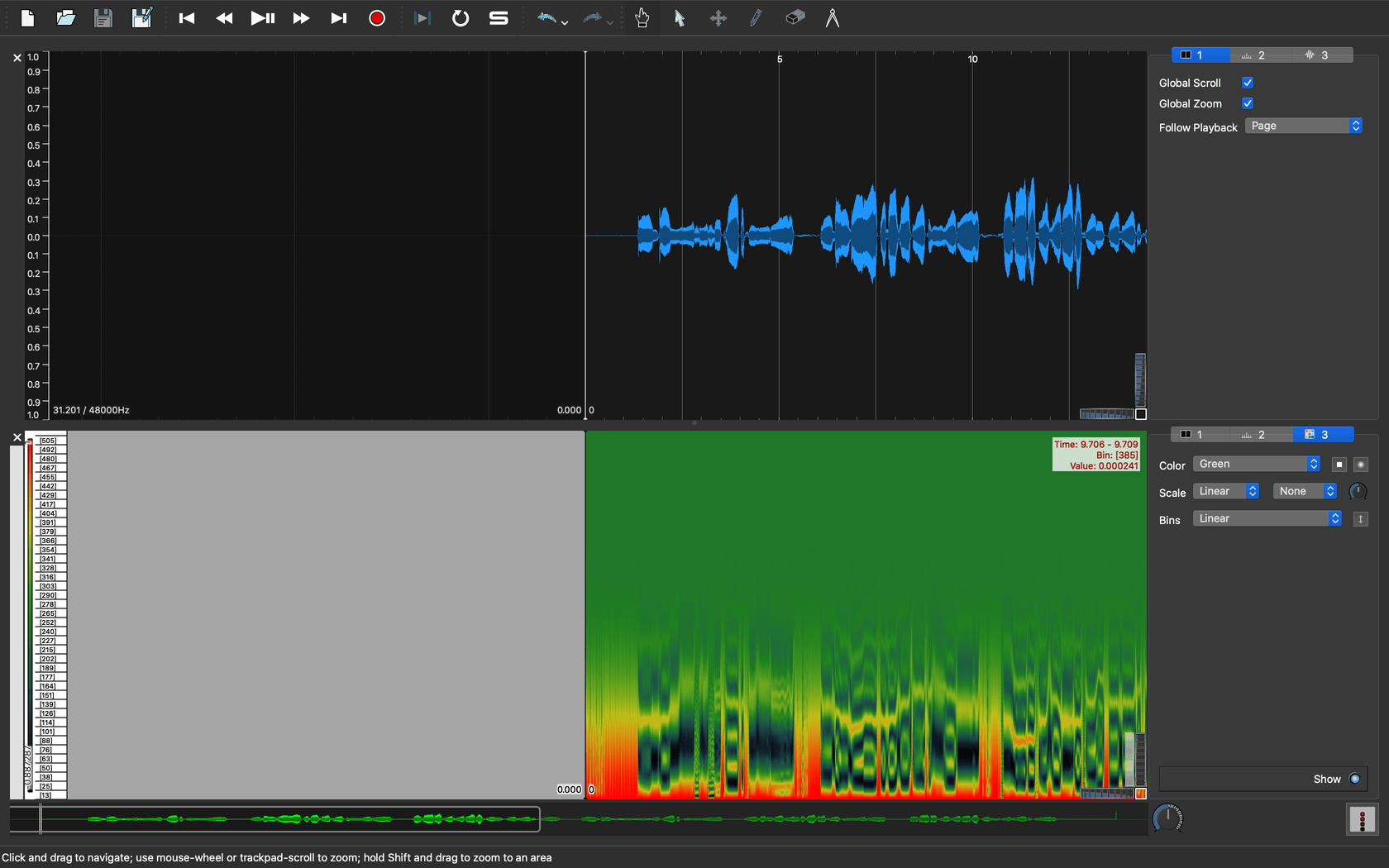図4. 時系列自己相関関数の可視化

私は単純に強弱を知りたいので白黒にすることが多いです。カラーマップに「White on Black」をよく利用しています。

図5. カラーマップをWhite on Blackに変更した

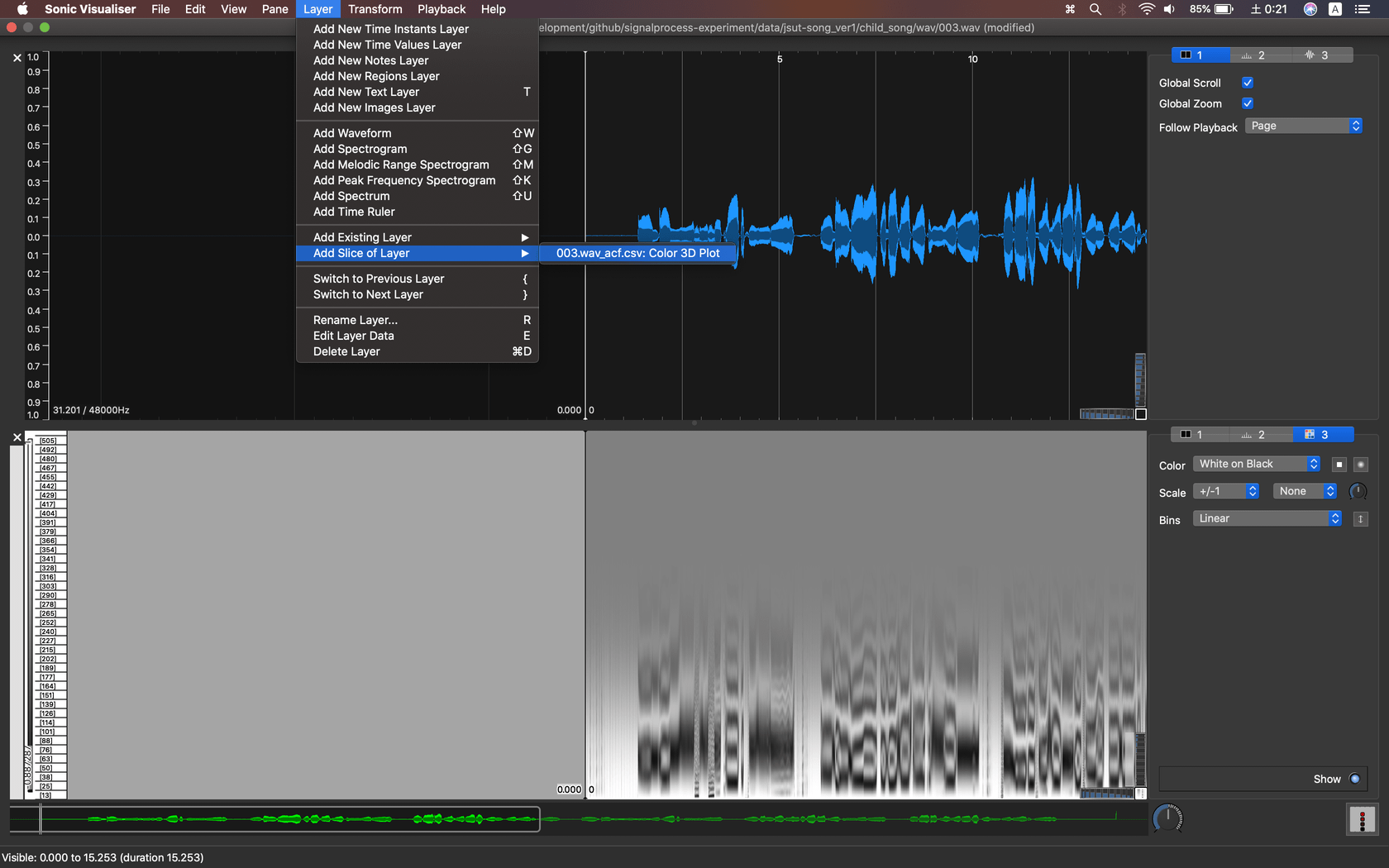
次に、メニューの「Layer」「Add Silece of Layer」から「003.wav_acf.csv: Color 3D Plot」を選択し、新しい表示レイヤーを自己相関関数を表示しているペインに追加します。これは、読み込んだデータのスライス（断面グラフ）を重ねて表示する機能です。

現在のカーソル位置のデータをスライス表示するので、具体的にどのような形になっているのかを調べるのに便利です。ただし、欠点として負値はゼロ値に切り上げられて表示されてしまいます。

図6. 断面グラフを重ねて表示

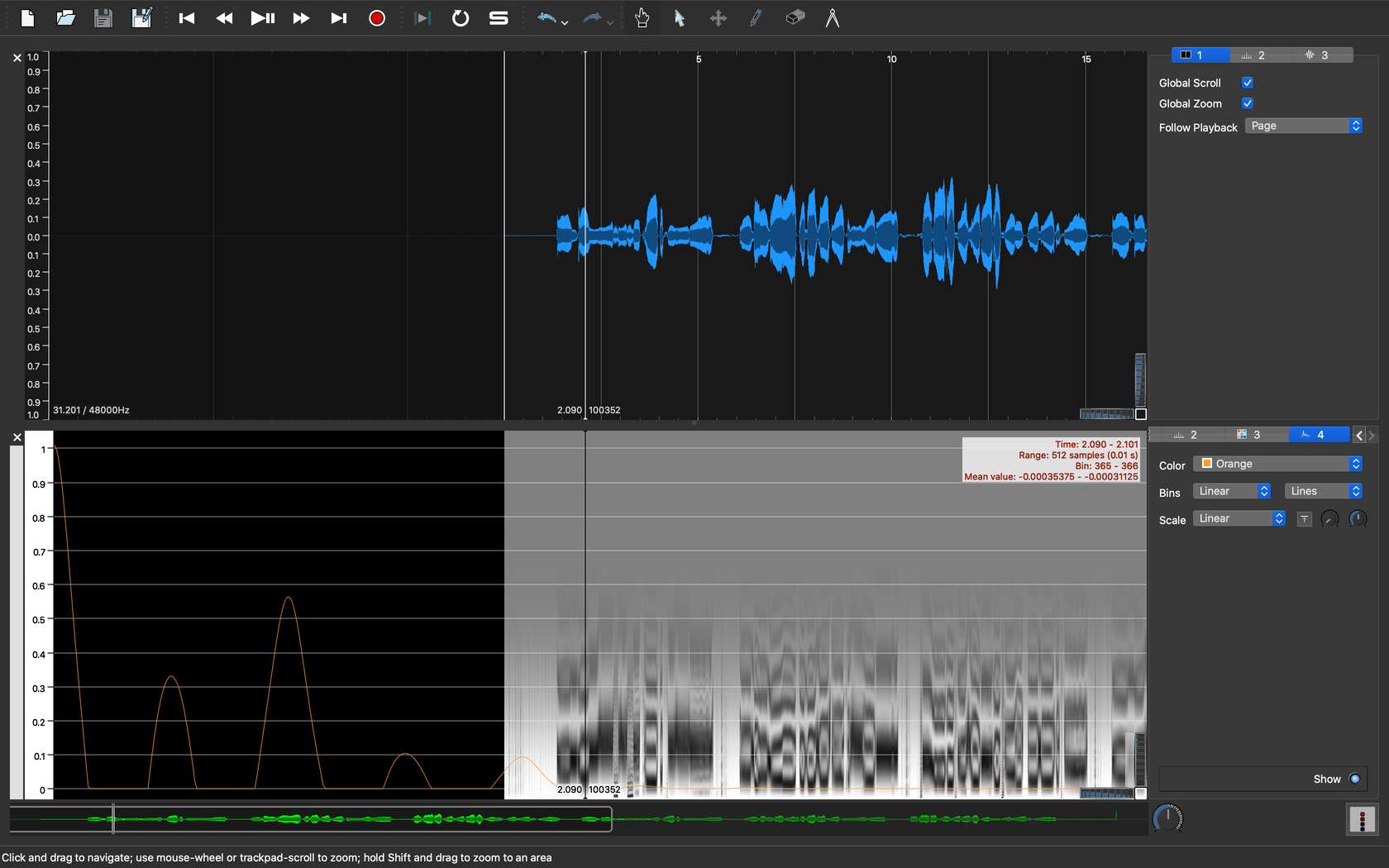
ここまでで可視化の方法は大体わかりました。実際に分析する際には気になるところにカーソルを移動して、断面図をみたり、前後フレームとの差を見たりします。

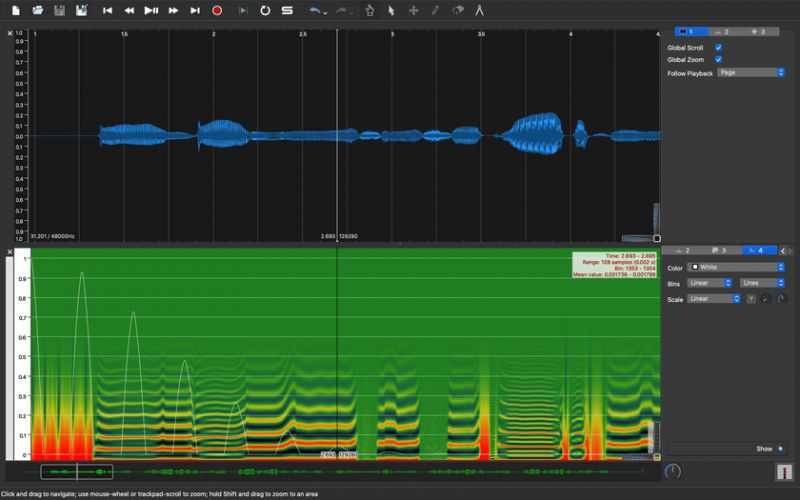
試しに歯擦音の場所の自己相関関数がどうなっているのかを見てみましょう。

図7. 歯擦音の自己相関関数

思ったよりも綺麗に倍音構造が見えており、ピッチが取れても仕方がない感じがします。

窓長2048サンプルで時系列自己相関関数データを出力し直す

そういえば、ピッチ推定ツールと同じでデフォルトの窓長は512サンプルでした。窓長に2048を指定してもう一度時系列自己相関関数データを生成しなおしてみます。

$ python time_series_acf.py -i ./data/jsut-song_ver1/child_song/wav/003.wav -w 2048

図8、図9が生成しなおしたデータを可視化した結果です。

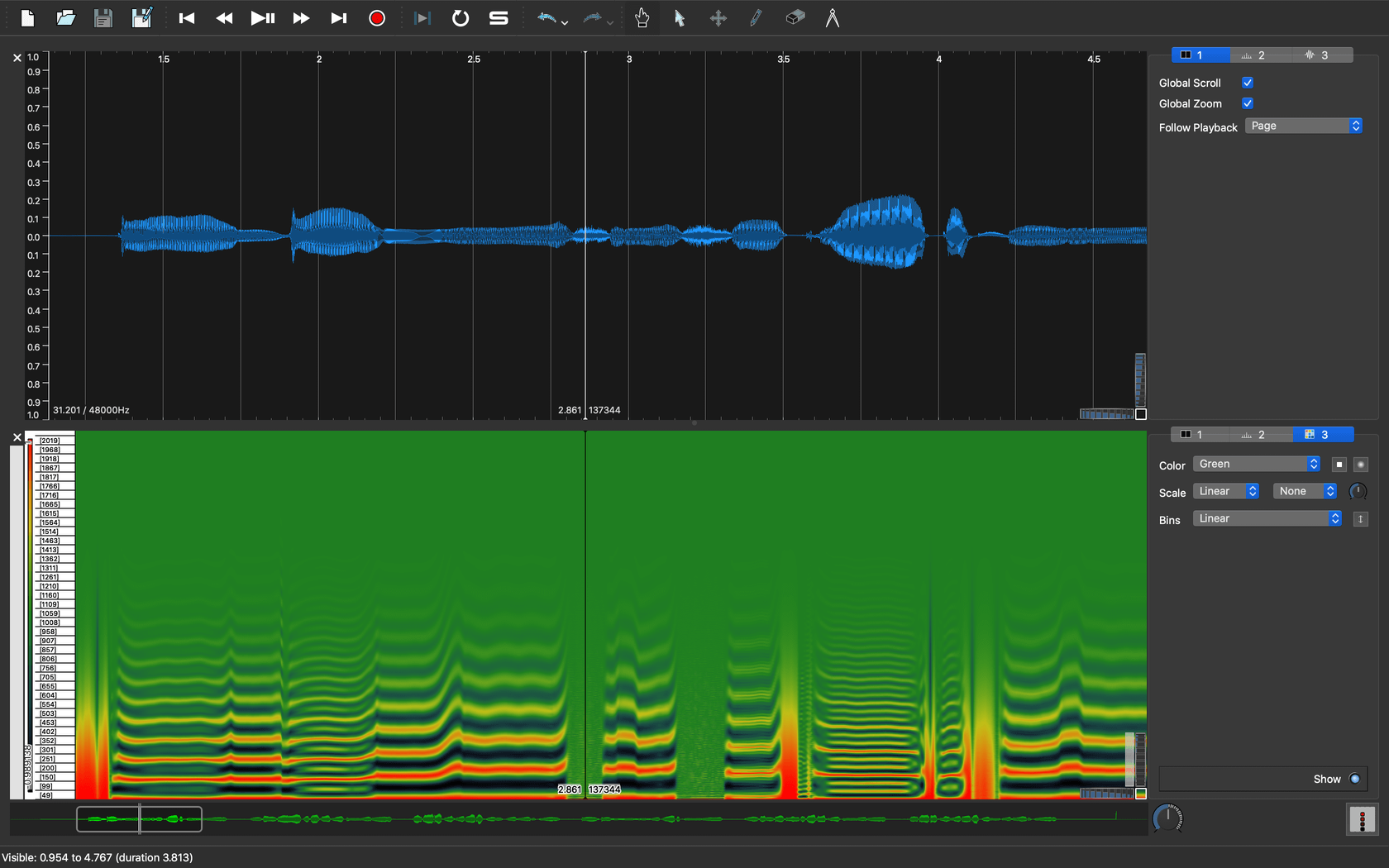図8. 窓長2048サンプルの時系列自己相関関数

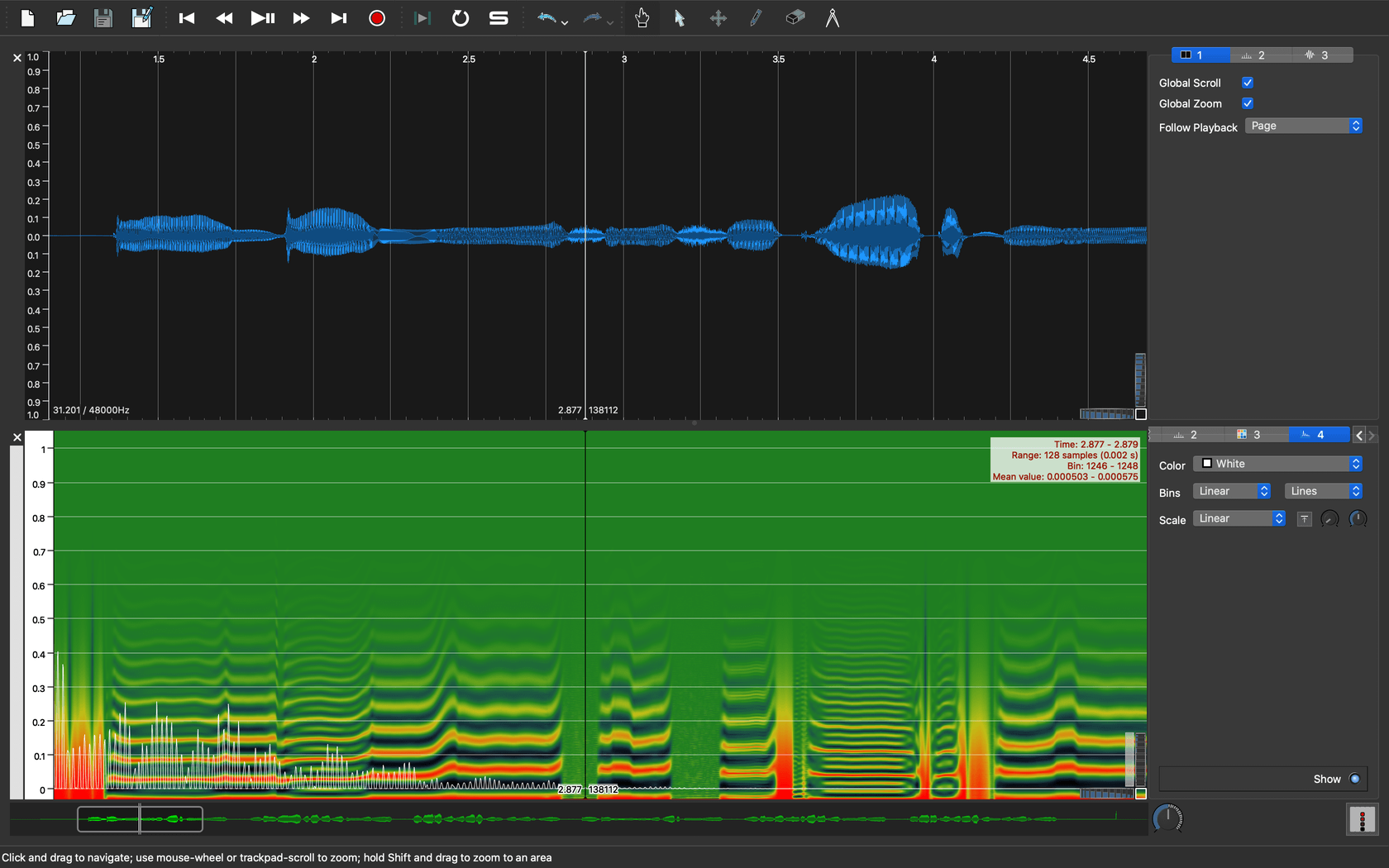窓長2048サンプルで求めた歯擦音の自己相関関数

窓長を長くすることで周波数分解能が上がったせいか、非常に細かい倍音成分を含んでおり、基本周期も高く、そもそも基本周期の相関係数が低いことがわかります。周波数分解能が低いまま解析すると、この櫛状の細かい成分がいくつかの周波数成分に集約されてしまい、そこそこはっきりした倍音構造を持ってるように見えてしまうので、オクターブミスを生じたり、無声音なのにピッチ信頼度（ここでは単に相関係数）が高くなってしまうということがわかります。

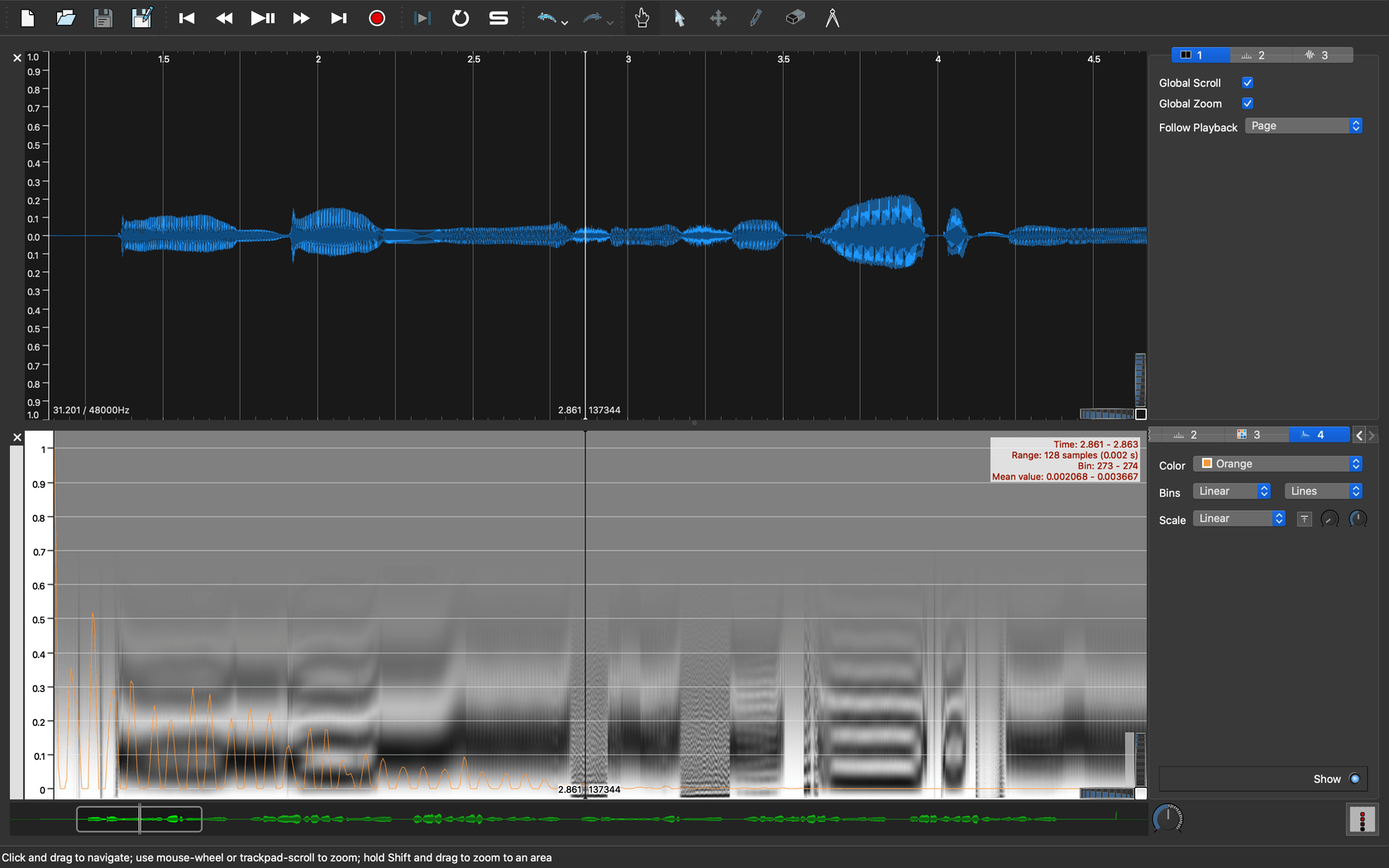
歯擦音の少し手前の母音部分の自己相関関数を表示してみると、図10のようにはっきりとした倍音構造が現れます。

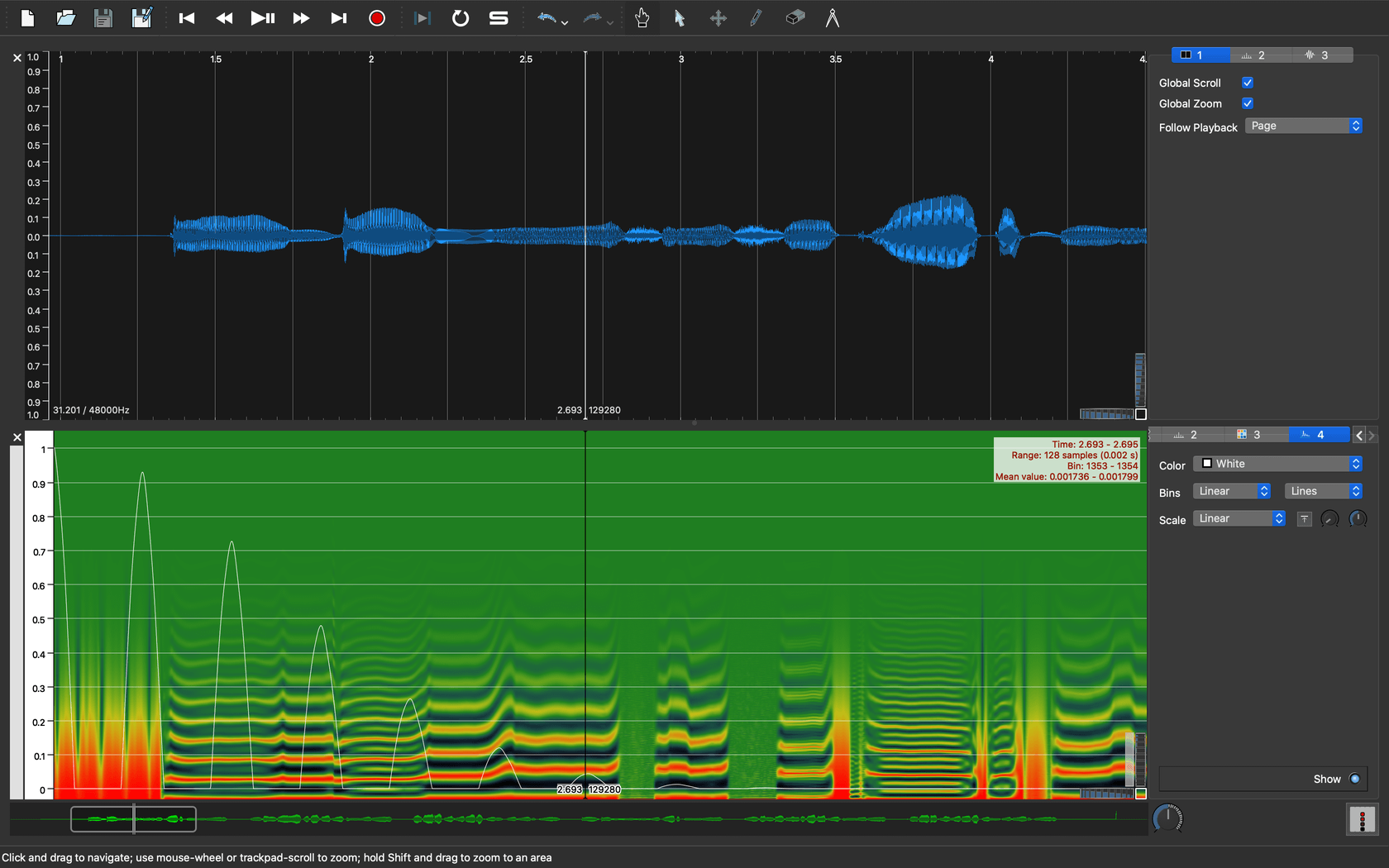図10. 窓長2048サンプルで求めた母音の自己相関関数

さて、自己相関関数によるピッチ推定は考え方がシンプルでわかりやすく、処理も単純でここまではっきりと良い結果が出るので、もうこれで十分に見えますが、それでもやはりピッチの推定が難しい波形は存在します。

毎回図10のように最初の山が基本周期とは限らない例が図11です。

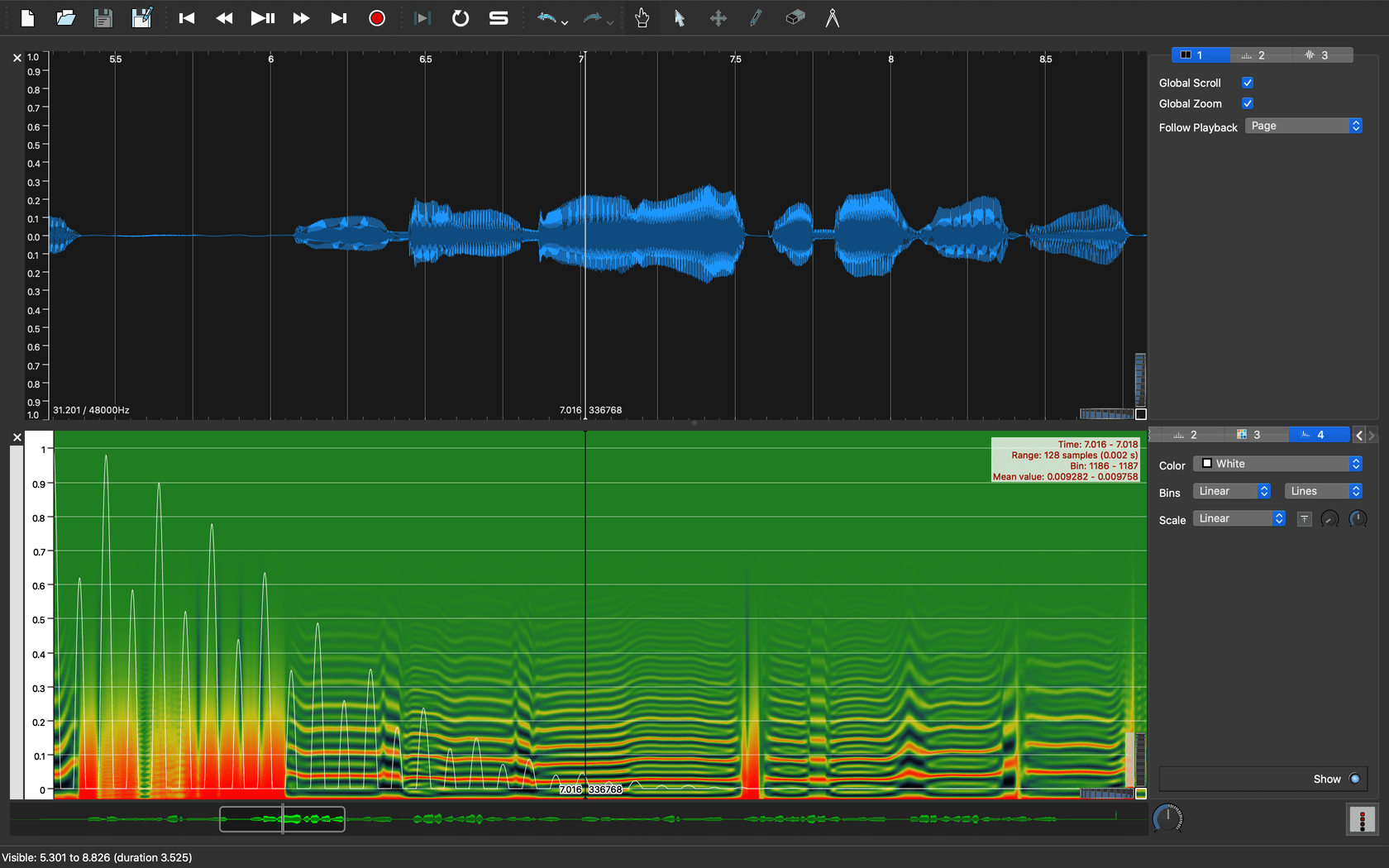図11. 二重ピッチのような形状

実際にこれが二重ピッチという事ではないですが、少し解析の方法を間違えると最初の低めの山を基本周期とみなしてしまい、本来の基本周期の約半分、周波数にして二倍、つまり１オクターブ分のピッチ誤推定が生じます。

実際の二重ピッチはもっと状況がひどく、二つの倍音構造がクロスフェードする瞬間だったりします。また、微妙な声道フィルタのかかり具合によっては、基本周期の半周期側が微妙に強く出てしまいオクターブミスが発生する場合もあります。

時系列データを視覚的に分析することで、ピッチ誤推定の原因を調査しやすくなります。

断面グラフ表示について補足

Sonic Visualiserの「Silece of Layer」は非常に優秀ですが、前述の通り負値を表示できません。できる方法があれば教えていただきたいです。

この問題に対する一つの答えは、全ての値は正になるようにオフセットを足してしまう事です。値を素直に解釈できなくなるので少し不便ですが、「視覚的にわかる」事が重要であればやってしまっても良いでしょう。

今回は自己相関関数-1 \sim 1なので、全体に1を足して2で割れば、0 \sim 1の範囲へ値を変換でき、Sonic Visualiserの「Silece of Layer」で全体を表示できるようになります。

def __acf(fragment, window_function):
    windowed = numpy.multiply(fragment, window_function)
    padded = numpy.r_[windowed, numpy.zeros(len(windowed))]
    acf = __acf_by_dft(padded)[:len(windowed)]
    if acf[0] != 0:
        acf /= acf[0]
    acf += 1 # オフセット
    acf /= 2 # 正規化
    return acf

おわりに

今回は分析を主眼においた内容でした。Pythonでpyplotを使えば自分で可視化するプログラムを作成するのはそこまで難しくないですが、スクロールできたり元音声を再生できたりするところまで作り込むのはなかなか骨が折れます。

そもそも目的は分析用GUIツールを作ることではなく、音声の分析そのものだったりするので、可視化にはSonic Visualiserのような既存の便利なツールを使う方が効率的に研究を進められるでしょう。

また、今回も実験に利用したJSUT-Songのような一定品質のデータが公開されていると、個人で研究や実験する際に実験データで迷わずにすみますし、他の研究者と実験結果を比較しやすくなるので大変重宝します。