はじめに

DFTを使った巡回畳み込み積分の性質をもう少し詳しく調べ、具体的な高速化のアイディアを紹介します。

実験

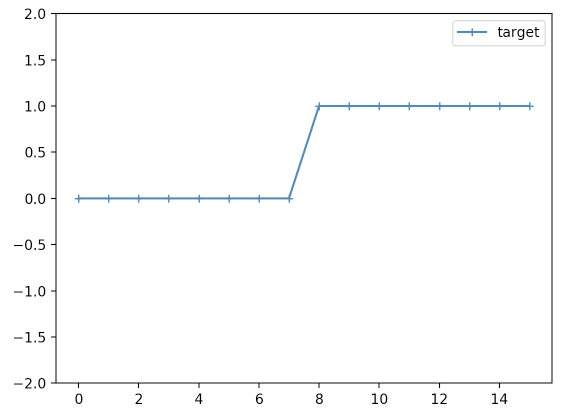
単純なステップ信号に対して差分フィルタ的なカーネルを畳み込む実験をしてみます。
畳み込み方法は、DFTによる方法、numpy.convolveのfullとvalidです。

import numpy
import scipy.fftpack
import matplotlib.pyplot as plt

def __convolve_by_dft(target, kernel):
    fft = scipy.fftpack.fft
    ifft = scipy.fftpack.ifft
    convolved = numpy.real(ifft(fft(target) * fft(kernel)))
    return convolved

def __single_plot(values, label_name, y_lower, y_upper):
    plt.plot(values, label=label_name, marker="+")
    plt.ylim(y_lower, y_upper)
    plt.legend()
    plt.show()
    plt.close()

if __name__ == "__main__":
    target = numpy.zeros(16)
    for i in range(0, 16, 8):
        target[i:i+8] = i // 8
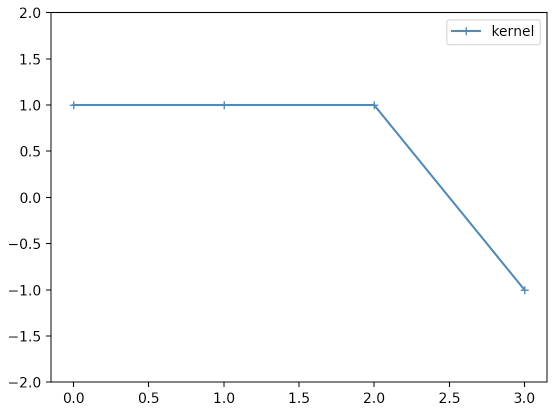
    kernel = numpy.array([1,1,1,-1])
    dft_convolved = __convolve_by_dft(target, numpy.r_[kernel, numpy.zeros(12)])
    numpy_full_convolved = numpy.convolve(target, kernel, mode="full")
    cyclic_target = numpy.r_[target[-(len(kernel) - 1):], target]
    numpy_valid_convolved = numpy.convolve(cyclic_target, kernel, mode="valid")

    __single_plot(target, "target", -2, 2)
    __single_plot(kernel, "kernel", -2, 2)

    plt.plot(target, label="target", marker="v")
    plt.plot(dft_convolved, label="by DFT", marker="o")
    plt.plot(numpy_full_convolved[:16], label="by Numpy(Full)", marker="x")
    plt.plot(numpy_valid_convolved[:16], label="by Numpy(Valid)", marker="+")
    plt.legend()
    plt.show()
    exit()

ステップ信号です。

フィルタカーネルです。

各手法による畳み込み積分の結果です。

考察

numpy.convolveのフィルタカーネルの仕様

numpy.convolveに指定したフィルタカーネルは、配列要素 $0$ が時刻 $0$ 、配列要素 $1$ が時刻 $-1$ を表しています。そのため、指定したフィルタカーネルは配列の逆順に畳み込まれます。
ステップ信号のエッジ部分で畳み込みの結果が負値になっていない事からも、フィルタカーネル配列が逆順に畳み込まれている事がわかります。

DFTによる畳み込みとfullモードのnumpy.convolveの結果の差

DFTによる畳み込みと、fullモードのnumpy.convolveの結果が微妙に異なります。
fullモードのnumpy.convolveは、フィルタカーネルと対象信号のそれぞれ端から端までを畳み込みます。足りない部分については $0$ 値を埋めて処理します。信号長 $M$ に対してフィルタカーネル長 $N$ で畳み込むと、結果は $M+N-1$ の要素数になります。対象信号の前後に $N-1$ の長さ分の $0$ 値をそれぞれ追加して処理します。そのため、同様の $0$ 値連結操作を行った対象信号に対するvalidモードのnumpy.convolveの結果と同じ結果になります。

今回の実験例ではフィルタカーネル長が $4$ なので、対象信号の先頭に $0$ 値が $3$ 要素分自動で追加され、 $[0,0,0,0]$ と $[-1,1,1,1]$ の内積を計算した結果になっています。つまり $0$ です。

しばらく $0$ 値の結果が続いた後、エッジ部分にフィルタカーネルが差し掛かり、 $[0,0,0,1]$ と $[-1,1,1,1]$ との内積計算により、結果が $1$ となります。そこからさらに処理を進めていった結果は以下の通りです。

$[0,0,1,1]$と$[-1,1,1,1]$との内積計算により結果は$2$
$[0,1,1,1]$と$[-1,1,1,1]$との内積計算により結果は$3$
$[1,1,1,1]$と$[-1,1,1,1]$との内積計算により結果は$2$

最終的には、フィルタカーネル長を $N$ とした場合に $N-1$ 分だけはみ出して内積計算します。今回の実験例では $N=3$ のため、末尾に $0$ 値を $3$ 要素分連結し、 $[1,0,0,0]$ と $[-1,1,1,1]$ との内積計算を行い、結果は $-1$ となります。末尾から遡った計算結果は以下の通りです。

末尾 $-0$ の要素の計算結果は $[1,0,0,0]$ と $[-1,1,1,1]$ との内積計算により $-1$
末尾 $-1$ の要素の計算結果は $[1,1,0,0]$ と $[-1,1,1,1]$ との内積計算により $0$
末尾 $-2$ の要素の計算結果は $[1,1,1,0]$ と $[-1,1,1,1]$ との内積計算により $1$
末尾 $-3$ の要素の計算結果は $[1,1,1,1]$ と $[-1,1,1,1]$ との内積計算により $2$

これらの結果とDFTによる畳み込みの結果を比べると、先頭 $3$ 要素の結果が異なる点と、fullモードのnumpy.convolveは末尾 $3$ 要素分余計に結果が出てきています。

対象信号長を $M$ 、フィルタカーネル長を $N$ とすると、DFTによる畳み込みの結果との一致範囲は要素インデックスをゼロオリジンとすると $N \sim M-1$ の $M-N + 1$ 要素、今回の実験では $M=16$ 、 $N=4$ なので $13$ 要素が一致します。

DFTによる畳み込みとvalidモードのnumpy.convolveの結果の比較

DFTによる畳み込みとfullモードによるnumpy.convolveの結果は、先頭 $N-1$ 要素が異なるのでした。それでは、DFTによる畳み込みでは、先頭 $N-1$ 要素はどのように算出された値で埋められているのでしょうか？

DFTによる畳み込みは巡回畳み込み積分でした。そのため、対象信号の末尾 $N-1$ 要素分を先頭に連結してからvalidモードのnumpy.convolveで畳み込みを計算します。

そうすると、先頭 $N-1$ の部分についてもDFTの畳み込みの結果と一致します。フィルタカーネルがはみ出す領域を、対象信号の巡回によって作り出して畳み込んだ結果が、DFTによる畳み込みの結果という事になります。

信号の任意長切り出しとゼロ値連結

DFTを使った畳み込み積分の高速化の方法を、overlap-save法と呼ぶようです。前述の通り、DFTによる畳み込み積分の結果の先頭 $N-1$ の要素は巡回部分なので使えません。よって、この使えない部分を手前のフレームで算出する事にします。そうなると、フレーム切り出しをオーバーラップして行う事になります。先頭 $N-1$ 分だけ使えないので、フレーム間のオーバーラップは $N-1$ 要素分です。

本気で高速化するのであれば、SIMDアラインメントやキャッシュラインサイズ、また、DFTをFFT高速化する場合は2のべき乗である必要などを考慮して、 $N-1$ が高速化に都合の良い値になるようにフィルタカーネル長 $N$ を決める必要があります。しかし、これを素直に実装すると、FIRフィルタの設計に制限が生じてしまいます。

そこで、正しく計算できている部分も余分に捨ててしまい、手前フレームの結果を使ってしまおうと割り切れば、実際のFIRフィルタに対して末尾に $0$ 値を連結して都合の良い長さにしてしまっても構いません。

ゼロ値と内積

余談になりますが、誤解を恐れずに言えばベクトル成分中の $0$ 値は内積の結果に影響を与えない成分だと言えます。そのため、内積や行列積を高速に計算するために、都合の良い次元数になるように $0$ 値を挿入するという計算テクニックがあります。

おわりに

今回はさらに一歩踏み込んで畳み込み積分をDFTで高速化する方法について実験を通して確認してみました。

実装にあたっては、オーバーラップサイズやフィルタカーネル長をどのように設計すれば良いか、世の中に情報が出回っているので、それらを参考にすると良いです。

基本的な考え方は本記事でも紹介した通りなので、まずは自分で試行錯誤してみるのも勉強になると思います。