はじめに

信号処理は解析学だけではなく統計学を必要とすることもあります。信号処理を抽象化すれば、数列から何かしらの処理により特徴量を抽出する処理だと言えます。今回は趣向を変えて、線形回帰分析を取り扱って見ます。

最小二乗モデルに基づく回帰直線

結論から言うと、最小二乗モデルに基づく回帰直線は、以下の方法で求めることができます。

$x$ が入力値、 $y$ が予測値だとして、線形回帰直線の一次関数を以下に定義します。

$y = a + b * x$

この一次関数の係数 $a$ と $b$ を求めれば良く、その方法は以下の通りです。

$\begin{aligned} b &= \frac{xとyの共分散}{xの分散} \\ a &= yの平均 – b * xの平均 \end{aligned}$

こんな単純な計算で本当に観測データに当てはまりの良い一次関数の係数 $a$ と $b$ が得られるのか、実験して見ましょう。

実験

python + Numpyで以下の通りに実験して見ました。

import sys
import numpy
import scipy
import matplotlib.pyplot as plt

def covariance(x_array, y_array):
    x_mean = numpy.mean(x_array)
    y_mean = numpy.mean(y_array)
    return numpy.dot((x_array - x_mean), (y_array - y_mean)) / x_array.size

def linear_regression_analysis(x_array, y_array):
    b = covariance(y_array, x_array) / numpy.var(x_array)
    a = numpy.mean(y_array) - b * numpy.mean(x_array)
    return b, a

if __name__ == "__main__":
    N             = 100
    noise_level   = 10

    true_data     = numpy.linspace(5, 60, N)
    noise_data    = scipy.randn(N) * noise_level
    observed_data = true_data + noise_data
    x_array       = numpy.array(range(0, N))

    b, a = linear_regression_analysis(x_array, observed_data)
    estimated = numpy.array([a + b * x for x in x_array])

    plt.plot(true_data,     label="True data")
    plt.plot(observed_data, label="Observed")
    plt.plot(estimated,     label="Estimated")
    plt.legend()
    plt.show()

    sys.exit(0)

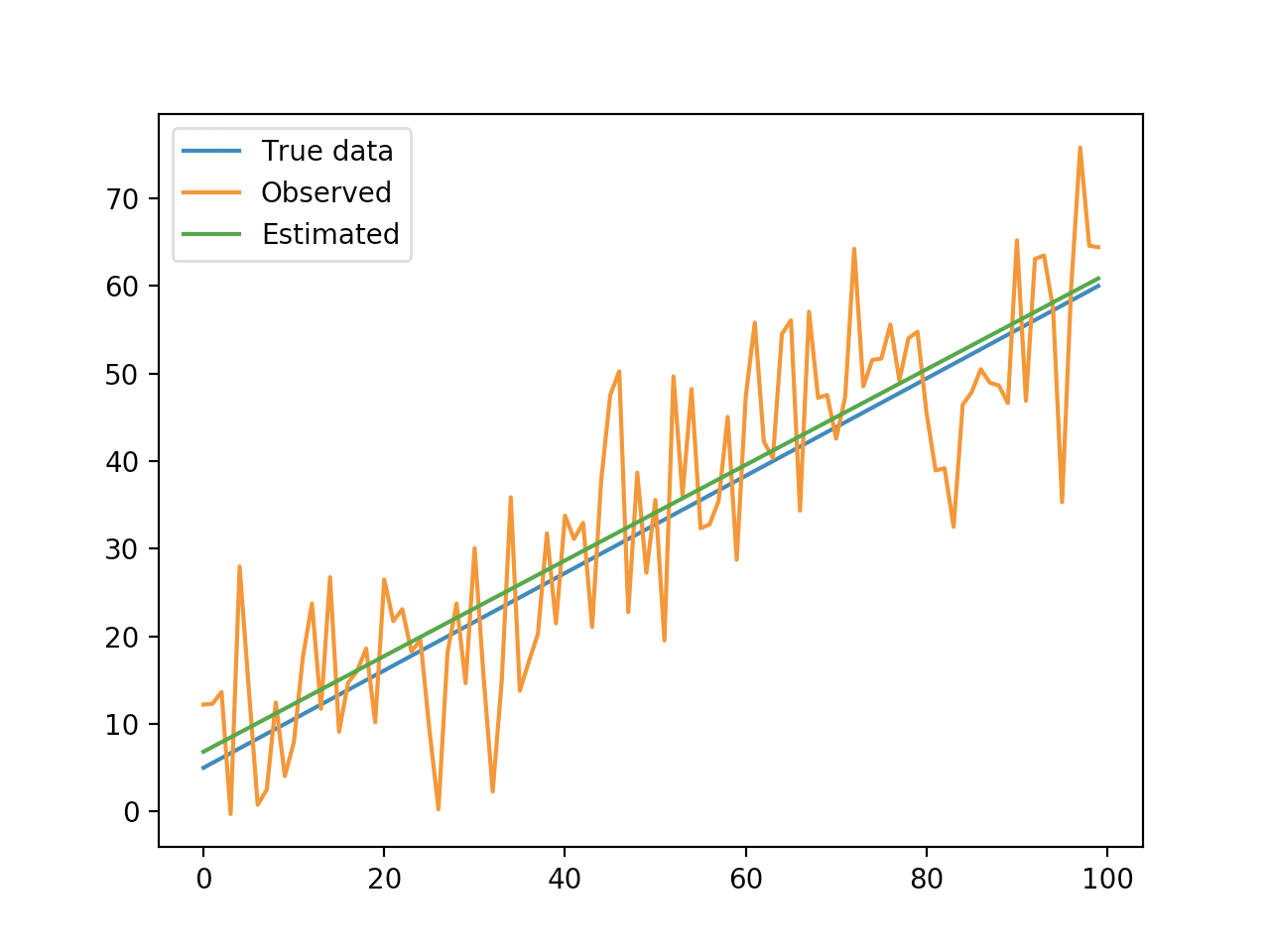
結果のグラフです。

covariance関数は共分散を求める関数です。共分散にはどうやら標本共分散と不偏共分散の二つの定義があるようですが、ここでは標本共分散を用いています。linear_regression_analysis関数が、まさに線形回帰分析関数です。回帰直線の係数 $a$ と $b$ を求めています。

結果のグラフから分かる通り、真のデータに近い予測値を観測データから得ることができています。といっても今回は、弱いノイズを直線のデータに足し合わせただけなので、割と良い結果になっています。実際の観測データでここまで良い結果になることはあまりありません。

Numpyにも共分散を求めるnumpy.cov関数がありますが、numpy.covは正確には不偏共分散を用いた分散共分散行列を計算する関数です。上記の独自実装の共分散関数とは結果が微妙に異なります。

一般に、観測データにはノイズが含まれるため、観測データをそのまま分析してしまうと、その解釈にノイズ成分も含めてしまうことになります。何かを観測する事は、自然科学においては観測データの裏にある母集団、ないしは信号源の性質、因果関係を知りたいためです。ノイズ成分を含んだまま観測データを解釈してしまうと、そこから導き出した因果関係の理論が、別の観測データにはほとんど当てはまらない、といった事が起こります。

実際のところ、観測データのみからノイズ成分を完璧に除去する方法はありません。完璧では無いにしろ、ある程度の妥当性を持ってしてノイズ成分を弱めることはできます。線形回帰分析はそういったある程度妥当な母集団予測方法の内の一つです。

誤差関数の選択

ところで、線形回帰分析では、回帰直線の係数aとbを求める式の導出において、二乗誤差と言う指標を定義します。二乗誤差とは、観測データと回帰直線との間の差を二乗して総和した値です。線形回帰分析では、この二乗誤差を最小化するように回帰直線の係数aとbを求めます。

単純に考えて、差の総和、差の絶対値の総和ではダメなのか？と言う疑問が湧くかもしれません。少なくとも私はそういった疑問を持ちました。

$\begin{aligned} 差の総和 &= \sum{x_a – x_b} \\ 差の絶対値の総和 &= \sum{|x_a – x_b|} \\ 二乗誤差 &= \sum{(x_a – x_b)^2} \end{aligned}$

差の総和

まず、差の総和ですが、正の値と負の値が釣り合うと、差の総和はゼロになってしまいます。二つの交わる直線について、その交点でどちらかの直線を回転させると、差の総和は常にゼロですが、直線同士は全く異なる傾きになってしまい、正しく予測できているとは言えない状態であっても誤差が最小ということになってしまいます。

差の絶対値の総和

次に、それなら差の絶対値の総和を求めれば良いのでは無いかと考えるかもしれません。この場合、確かに直線同士が重なるほど誤差は小さくなるのですが、では、その誤差が最小となるところはどのように求めれば良いでしょうか？ある関数の最小値を求めるためには、微分してゼロとなる点（極値）を探せば良いのでした。極値の内、全体で最小のものを最小値と言います。では、絶対値の総和関数が最小となる点を微分で求められるかというと、これは一次関数の絶対値をとっているので、最小となる点で微分不可能です。そのため、解析的には最小値となる点を求めることができません。

差の二乗総和

そこで、差を二乗して総和する二乗誤差の出番です。二乗誤差は、差の二乗を計算しているため常にゼロ以上の値となり、関数の外形は下凸の二次関数になります。二次関数なので、全域で微分可能であり、極値も全域で一つしか存在しないため、微分して極値を求める事が簡単になります。

多くの予測問題、近似問題で二乗誤差を誤差量の指標に使うのは、最小値を解析的に求めやすいためだと言えます。

また、差を二乗して総和を求めるということは、ユークリッド距離の二乗を求めている事に等しいです。つまり、最小二乗誤差とは、ユークリッド空間上での二つのベクトル間の距離の二乗を求めている事になるので、直感的にも理解しやすい指標だと言えます。