はじめに DFTで周波数変換する際に窓関数の概念は避けて通れません。今まで窓関数を使った事がないという方の場合、それは矩形窓を使っていた事になります。
Read more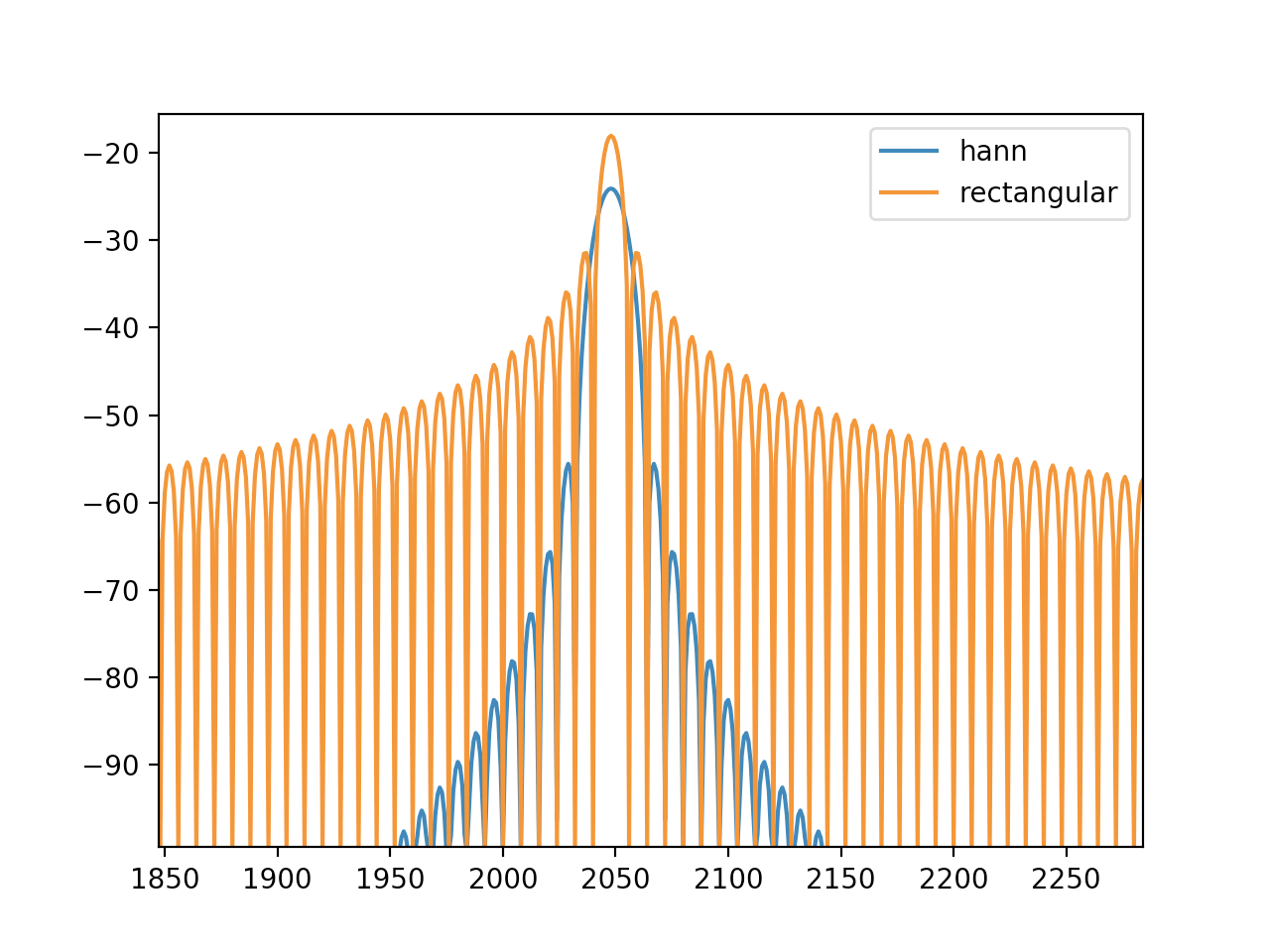
信号処理を勉強する

はじめに DFTで周波数変換する際に窓関数の概念は避けて通れません。今まで窓関数を使った事がないという方の場合、それは矩形窓を使っていた事になります。
Read more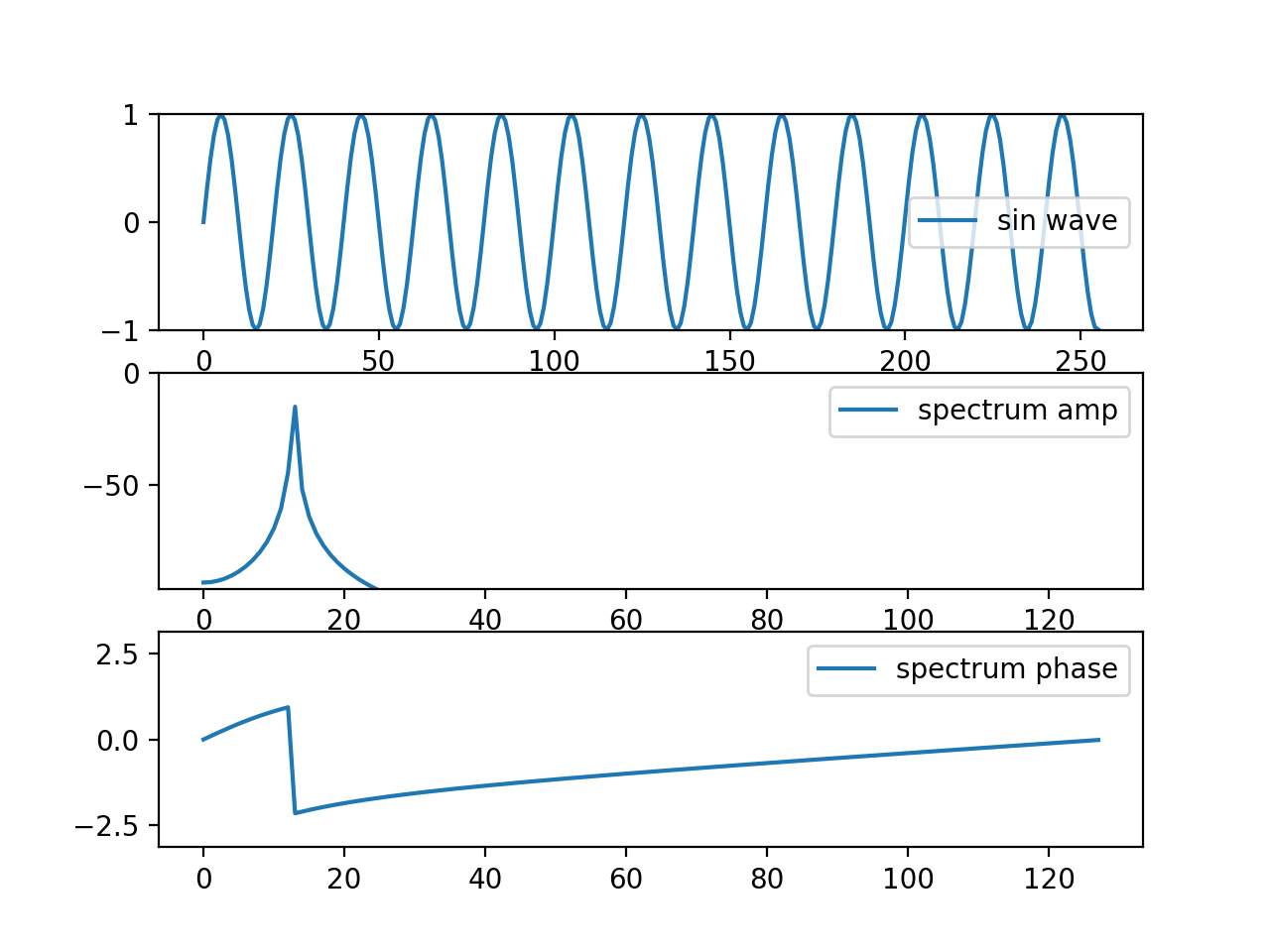
離散フーリエ変換は、窓長を1周期とする周期性のある波を最長とし、その整数倍周波数の足し合わせ表現に原信号を変換します。原信号が素直に整数倍の周波数のサイン波で構成されていれば、いわゆるサイドローブが現れず、綺麗な変換結果
Read more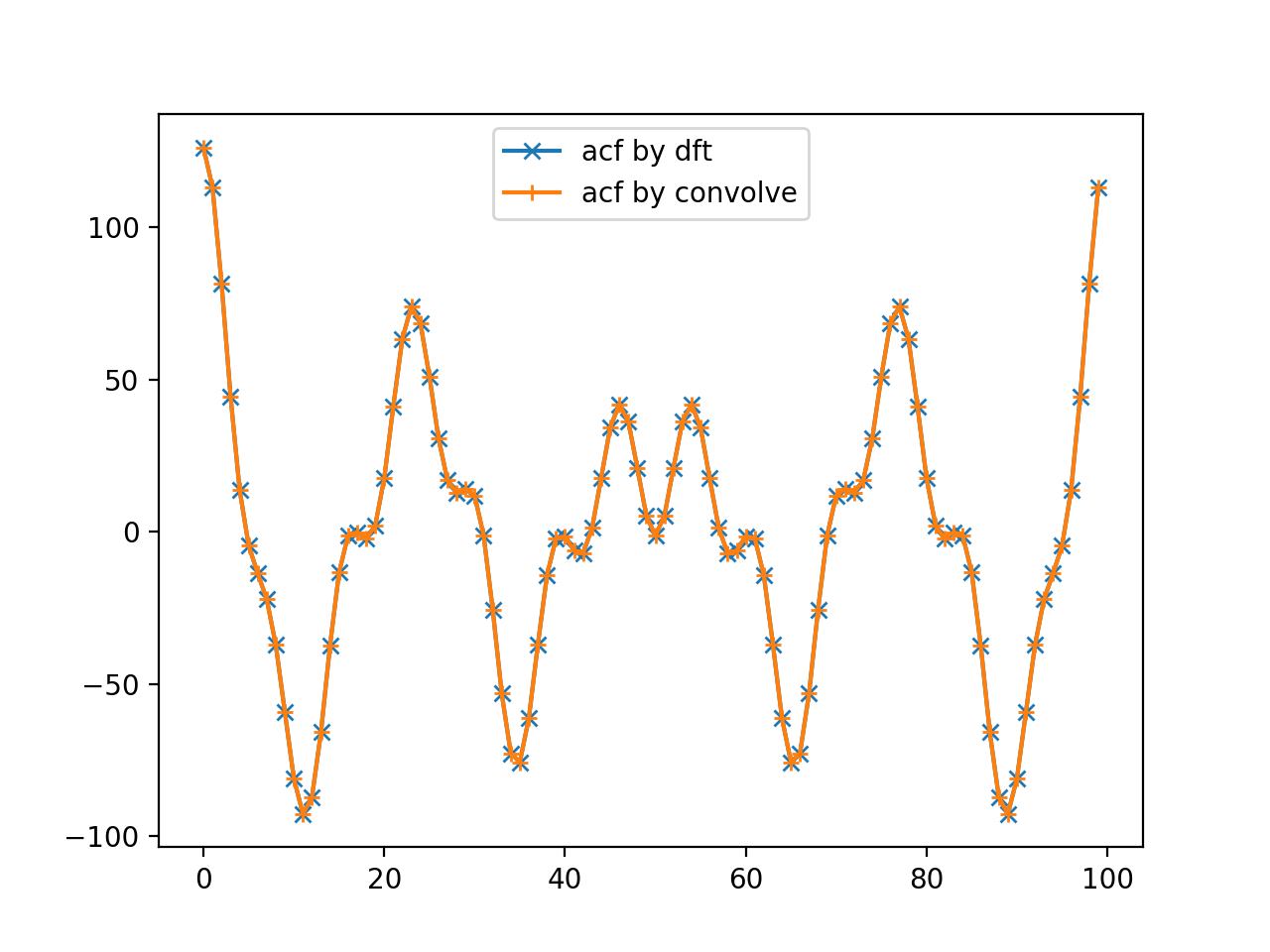
信号を分析する手法の一つに自己相関関数があります。対象とする信号の性質に応じて定義は複数存在しますが、有限長の離散信号に対しては、以下の式で定義する自己相関関数を用いることが多いです。
Read moreはじめに DFTの各基底ベクトルは複素ベクトルのため、DFTによって得られた結果も複素ベクトルです。つまり、結果の各要素は複素数であり、実部と虚部を持ちます。 結果の複素ベクトルの各要素に対して、複素数の大きさを計算した
Read more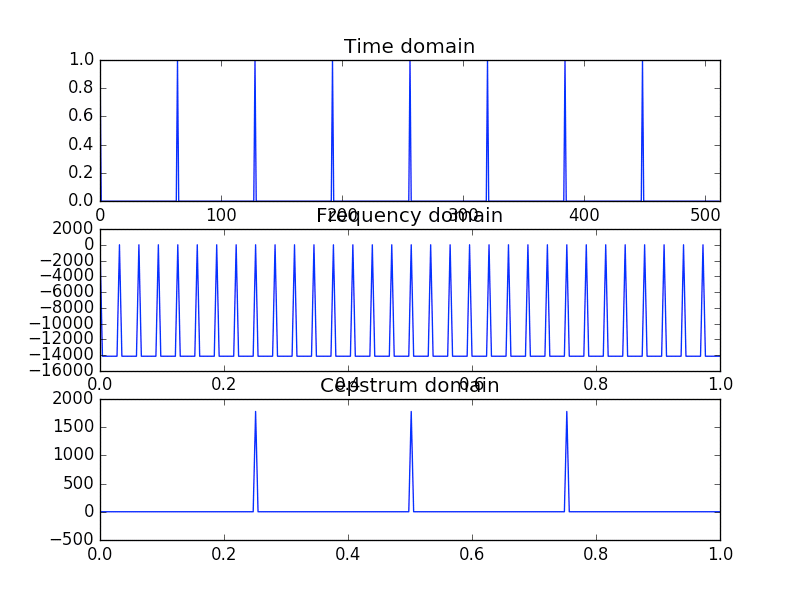
はじめに DFTで求めた振幅スペクトラムに対して、対数スケールに変換した後にIDFT(またはDFT)を施すことで、ケプストラムを得ることができます。 ここではくし状信号のケプストラムを求めてみます。
Read more