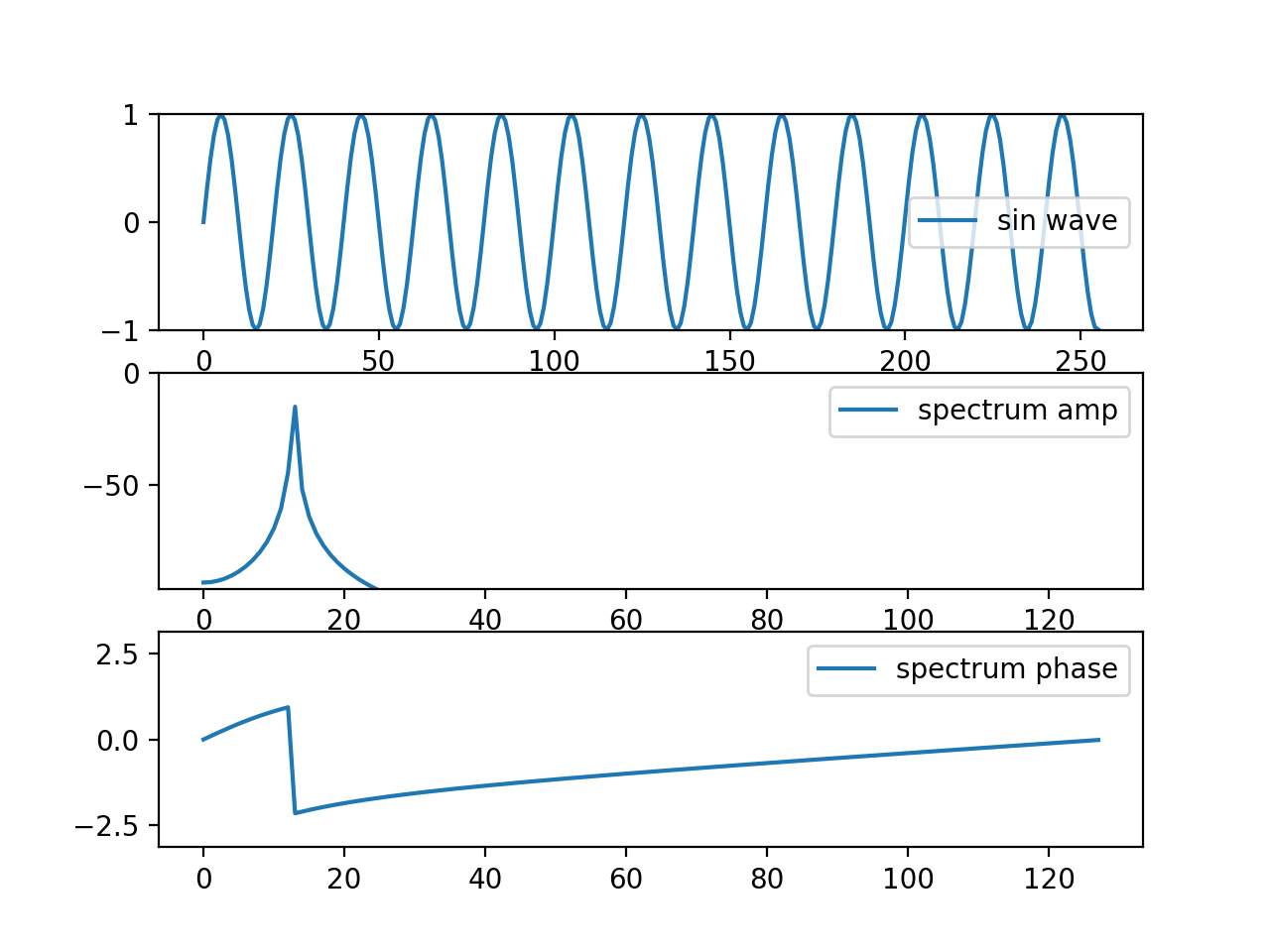
離散フーリエ変換は、窓長を１周期とする周期性のある波を最長とし、その整数倍周波数の足し合わせ表現に原信号を変換します。原信号が素直に整数倍の周波数のサイン波で構成されていれば、いわゆるサイドローブが現れず、綺麗な変換結果になります。

では、整数倍ではない周波数のサイン波成分は、振幅スペクトラムや位相スペクトラムにどのように現れるのでしょうか？

周波数スイープしながらDFTを施す実験

以下のコードは、窓長256サンプルとして、周波数1から64まで0.1きざみで変化させながらサイン波を生成し、DFTで振幅スペクトラムと位相スペクトラムを求めています。
求めた結果を周波数毎に、上から原信号のサイン波、DFT結果の振幅スペクトラム、位相スペクトラムの順に並べてアニメーションさせています。
周波数を少しずつ変化させながら、振幅スペクトラム、位相スペクトラムがどのように変化するのかを直感的に理解することができます。

import numpy
import sys
import scipy.fftpack
import matplotlib.pyplot as plt
import matplotlib.animation as anim

def make_sin(N, f):
    angles = numpy.linspace(0, N - 1, N) * 2 * numpy.pi * f / N
    return numpy.sin(angles)

if __name__ == "__main__":
    N = 256

    result_sin  = []
    result_amp_db = []
    result_phase = []
    max_f = int(N / 4)

    f_array = numpy.linspace(1, max_f, max_f * 10 + 1)

    for f in f_array:
        sin_vec = make_sin(N, f)
        sin_vec = sin_vec / numpy.linalg.norm(sin_vec)
        spectrum = scipy.fftpack.fft(sin_vec) / numpy.sqrt(N)
        spectrum_amp_db = 20 * numpy.log(numpy.abs(spectrum) + sys.float_info.min)[:int(N/2)]
        spectrum_phase = numpy.angle(spectrum)[:int(N/2)]
        result_sin.append(sin_vec)
        result_amp_db.append(spectrum_amp_db)
        result_phase.append(spectrum_phase)

    fig = plt.figure()
    subplots = []
    artists = []
    y_limit = [(-1,1), (-96, 0), (-numpy.pi, numpy.pi)]
    num_x = [range(N), range(int(N/2)), range(int(N/2))]
    labels = ["sin wave", "spectrum amp", "spectrum phase"]

    for i in range(0, 3):
        r = fig.add_subplot(3,1,i + 1)
        subplots.append(r)
        subplots[i].set_ylim(y_limit[i][0], y_limit[i][1])
        im, = subplots[i].plot(num_x[i], num_x[i], label = labels[i])
        subplots[i].legend()
        artists.append(im)

    def update(frame):
        i = frame % len(result_sin)
        artists[0].set_data(num_x[0], result_sin[i])
        artists[1].set_data(num_x[1], result_amp_db[i])
        artists[2].set_data(num_x[2], result_phase[i])
        return artists

    animation = anim.FuncAnimation(fig, update, interval=50, blit=True)
    plt.show()

    sys.exit(0)

非整数周波数の振幅値

実験の結果から、整数周波数のサイン波に対するDFT（離散フーリエ変換）の結果は、その周波数成分だけ振幅値が出ることがわかります。

一方、非整数の半端な周波数のサイン波に対するDFTの結果は、振幅値が両隣の整数周波数binに按分されています。
さらに、一見無関係な周波数binの振幅値も上昇しています。これがいわゆるサイドローブ成分です。

DFTは、実部に整数周波数のcos関数ベクトル、虚部に整数周波数のsin関数ベクトルを基底ベクトルとする直行変換なので、対象の信号に対して、整数周波数のコサイン波とサイン波それぞれについて内積を求めている事と同じです。
対象信号が単一の整数周波数のコサイン波、もしくはサイン波であれば、周波数binの一つだけが絶対値でゼロより大きい値になり、その他の周波数binは対象信号と直行する基底ベクトルによる内積の結果なので、値がゼロになります。

それでは、対象信号が単一の非整数周波数のコサイン波、もしくはサイン波だった場合、どうなるでしょうか？

対象信号が単一の非整数周波数のコサイン波、もしくはサイン波だった場合、全周波数binの値が絶対値でゼロより大きい値になります。
つまり、単一の非整数周波数のコサイン波、もしくはサイン波は、全ての整数周波数のコサイン波、およびサイン波に対して直行しなくなるのです。
さらに、上記コードを実行するとわかりますが、各周波数binに按分される振幅値は、対象信号である単一の非整数周波数のコサイン波、もしくはサイン波の周波数をピークとして、離れれば離れるほど減衰するように按分されていきます。
この特性は、他の直行変換とDFTを比較した際に、DFTの周波数領域における値の扱いやすさの一端ではないかと考えます。

非整数周波数の位相

振幅値がサイドローブの影響を受けるのと同様に、位相成分もサイドローブの影響を受けます。
位相は実部と虚部の比によって角度が決まります。そのため、振幅値が非常に小さな値だったとしても、位相には有効そうな値が現れてしまうところが厄介です。

位相については複雑なので、別の記事で詳細を調べます。