はじめに

DFTで求めた振幅スペクトラムに対して、対数スケールに変換した後にIDFT(またはDFT)を施すことで、ケプストラムを得ることができます。

ここではくし状信号のケプストラムを求めてみます。

具体的に計算する

import sys
import numpy
import scipy.fftpack
import matplotlib.pyplot as plt

if __name__ == "__main__":
    comb_parts   = numpy.r_[[1.0], numpy.tile([0.0], 63)]
    comb_signal  = numpy.tile(comb_parts, 8)
    spectrum     = scipy.fftpack.fft(comb_signal) / numpy.sqrt(len(comb_signal))
    spectrum_amp = 20 * numpy.log(numpy.absolute(spectrum) + sys.float_info.min)
    cepstrum     = numpy.real(scipy.fftpack.ifft(spectrum_amp - numpy.mean(spectrum_amp)))

    half_size = int(len(comb_signal) / 2)
    plt.subplot(3, 1, 1)
    plt.title("Time domain")
    plt.xlim(0, len(comb_signal))
    plt.plot(range(0, len(comb_signal)), comb_signal)

    plt.subplot(3, 1, 2)
    plt.title("Frequency domain")
    plt.xlim(0, 1)
    plt.plot(numpy.linspace(0, 1, half_size), spectrum_amp[:half_size])

    plt.subplot(3, 1, 3)
    plt.title("Cepstrum domain")
    plt.xlim(0, 1)
    plt.plot(numpy.linspace(0, 1, half_size), cepstrum[:half_size])

    plt.show()

    exit(0)

対数スケールに変換する際に、ゼロ除算例外が発生する可能性があります。対数スケールへの変換に使用するlog関数は、数学的なレベルで入力値ゼロのとき未定義です。入力信号が全ての周波数成分を含んでいれば問題ありませんが、どこかの周波数成分がゼロということは可能性としてはあり得ます。

そこで、log関数に入力する値に対して、極小の値を足しこむことで、この問題を回避しています。

また、平均値を引いていますが、これはスペクトラムの直流成分を取り除くために行っています。直流成分は交流成分と比較して大きい値が出てきます。グラフ化する際に値の範囲が大きくなってしまい、細かい値の変動を見づらくなってしまうので取り除いています。

最終的には、振幅スペクトラムにIDFTを施して得られる複素数列の実部のみを取り出した信号がケプストラムになります。

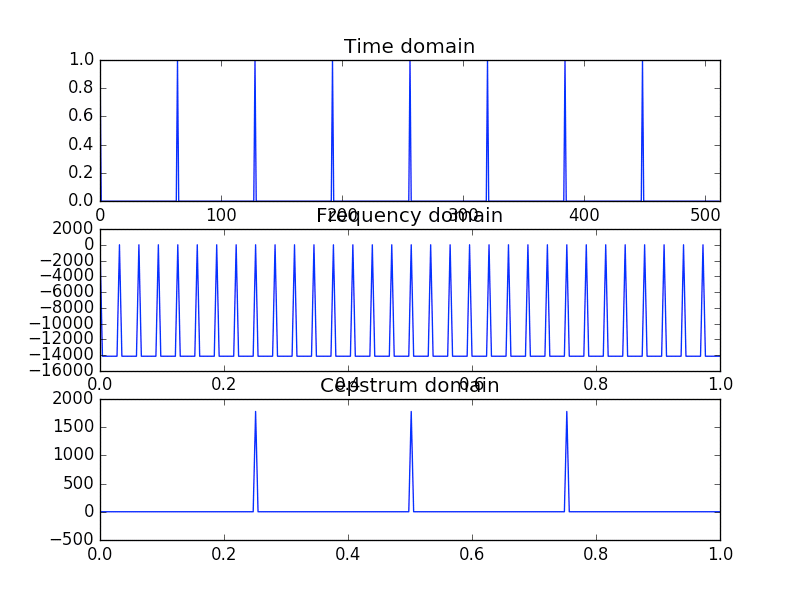
以下の画像は上記のスクリプトを実行して得られた、くし状信号のケプストラムをプロットした画像です。くし状の信号のケプストラムもやはりくし状になります。

おわりに

ちなみに、ケプストラムの虚部はどうなったのかというと、全てゼロ値になります。時間信号にDFTを施して得られる振幅スペクトラム成分は線対称形でした。その信号全体に対してDFT（またはIDFT）を施すと、計算途中に共役な成分が出現し、虚部は打ち消しあってゼロになります。

これはどうやらDCTに似ていそうです。