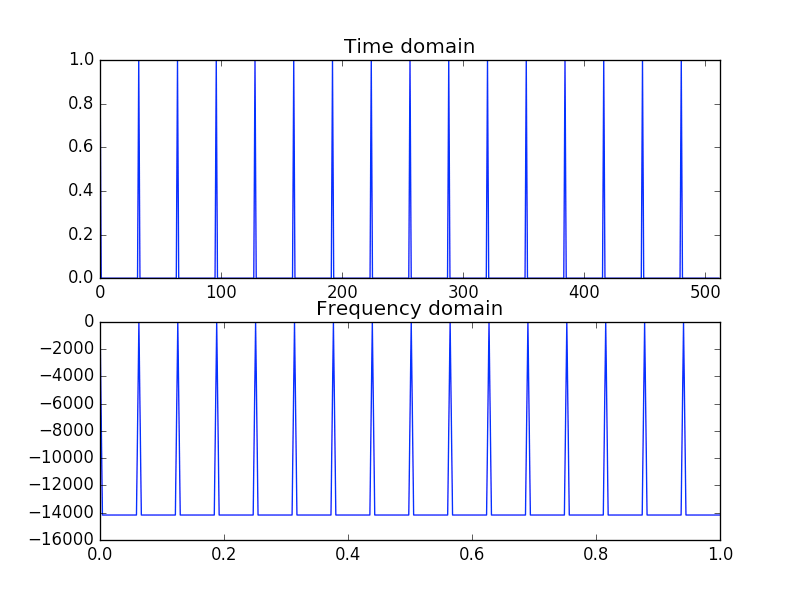
時間領域の単位インパルスにDFTを施すと、周波数領域ではフラットな振幅特性になります。
それでは、単位インパルスを一定間隔に並べた単位インパルス列にDFTを施すとどうなるでしょうか?
以下のpythonコードで実際に試してみましょう。
(Anaconda3のインストールも忘れずに!)
import sys
import numpy
import scipy.fftpack
import matplotlib.pyplot as plt
if __name__ == "__main__":
comb_parts = numpy.r_[[1.0], numpy.tile([0.0], 31)]
comb_signal = numpy.tile(comb_parts, 16)
spectrum = scipy.fftpack.fft(comb_signal) / numpy.sqrt(len(comb_signal))
amplitude_db = 20 * numpy.log(numpy.absolute(spectrum) + sys.float_info.min)
half_size = int(len(comb_signal) / 2)
plt.subplot(2, 1, 1)
plt.title("Time domain")
plt.xlim(0, len(comb_signal))
plt.plot(range(0, len(comb_signal)), comb_signal)
plt.subplot(2, 1, 2)
plt.title("Frequency domain")
plt.xlim(0, 1)
plt.plot(numpy.linspace(0, 1, half_size), amplitude_db[:half_size])
plt.show()
exit(0)
32サンプル毎に単位インパルスを配置した、全長512サンプルのくし状信号を生成し、DFTを施します。
実際にはFFT関数を使いますが、scipyのFFTは対象信号のサンプル数が2の冪乗ではなくても処理可能なので、実質的にはDFT関数です。
DFTの結果は複素数スペクトルなので、絶対値を計算することで振幅スペクトルを得ることができます。(角度を計算すると位相スペクトルを得ることができます。)
ワンライナーで書いていますが、振幅スペクトルの値をデシベル(dB)スケールに変換しています。(sys.float_info.minを足しているのは、対数関数にゼロを指定しないようにするためのワークアラウンドです。)
FFTによって得られる振幅スペクトルの値の数は、時間領域でのサンプル数と同じです。
ただし、実際には指定した数の半分からは線対称な値が得られるため、前半だけあれば振幅特性がわかります。
よって、振幅スペクトルの前半分だけをプロットしています。
図の通り、くし状信号にDFTを施した結果は、周波数領域でもくし状になることがわかります。
今回の実験ではサンプリングレートは特に決めていないため、周波数領域の横軸は正規化周波数です。
正規化周波数の1.0はおよそナイキスト周波数に該当します。サンプリング周波数では無い点に注意してください。(シャノン・染谷の標本化定理により、サンプリング周波数の半分未満までしか周波数成分を表現できません。)
もう少し抽象的に表現すると、くし状の信号にDFTを施した場合、変換先の領域でもくし状になる、ということです。